四川省甘孜藏族自治州2023年中考数学真题

更新时间：2024-04-19 浏览次数：121 类型：中考真卷

一、选择题(本大题共10个小题,每小题3分,共30分.每小题均有四个选项,其中只有一项符合题目要求)

1. (2024九下·南宁模拟) 下列各数中，最小的是（）

A . -2 B . 0 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
2. (2023·甘孜) 以下几何体的主视图是矩形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九下·济南模拟) “绿水青山就是金山银山”，多年来，某湿地保护区针对过度放牧问题，投入资金实施湿地生态效益补偿，完成季节性限牧还湿29.47万亩，使得湿地生态环境状况持续向好。其中数据29.47万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·甘孜) 以下图案中，既是轴对称图案又是中心对称图案的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024七下·任丘期末) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·甘孜) 如图，AB与CD相交于点 $\text{[math]}$ ，只添加一个条件，能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九上·云岩期中) 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示.
成绩/米
1.50
1.60
1.65
1.70
1.75
人数
2
3
5
4
1
这些运动员成绩的众数和中位数分别为（）

A . 1.65米，1.65米 B . 1.65米，1.70米 C . 1.75米，1.65米 D . 1.50米，1.60米

答案解析收藏纠错 + 选题
8. (2023·甘孜) 如图，点A，B，C在 $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·银川模拟) 有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛(斛，音hú，是古代的一种容量单位)，1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛？设大桶可以盛酒 $\text{[math]}$ 斛，小桶可以盛酒 $\text{[math]}$ 斛，则可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. 下列关于二次函数 $\text{[math]}$ 的说法正确的是（）

A . 图象是一条开口向下的抛物线 B . 图象与 $\text{[math]}$ 轴没有交点 C . 当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 增大而增大 D . 图象的顶点坐标是 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本大题共4个小题,每小题4分,共16分)

11. (2024七下·于都期中) 比较大小： $\text{[math]}$ 2.(填“<”或“>”)

答案解析收藏纠错 + 选题
12. (2023·甘孜) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个相等的实数根，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
13. (2023·甘孜) 若反比例函数 $\text{[math]}$ 的图象位于第一、三象限，则 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
14. (2023·甘孜) 如图，在平行四边形 $\text{[math]}$ 中，按如下步骤作图：①以点 $\text{[math]}$ 为圆心，以适当长为半径画弧，分别交AB，AD于点M，N②M，N为圆心，以大于 $\text{[math]}$ 的长为半径画弧，两弧在 $\text{[math]}$ 内交于点 $\text{[math]}$ ；③作射线AP交BC于点 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 为 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题(本大题共6个小题,共54分)

15. (2023·甘孜)
1. （1）计算： $\text{[math]}$ ；
2. （2）解不等式组： $\text{[math]}$
答案解析收藏纠错 + 选题
16. (2023·甘孜) 化简： $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2023·甘孜) 某校为开设足球、篮球、排球选修课程，现对该校学生就“你最喜欢的球类运动”进行抽样调查(要求在“足球”、“篮球”、“排球”中选择一种)，将调查数据绘制成如下的两幅统计图.
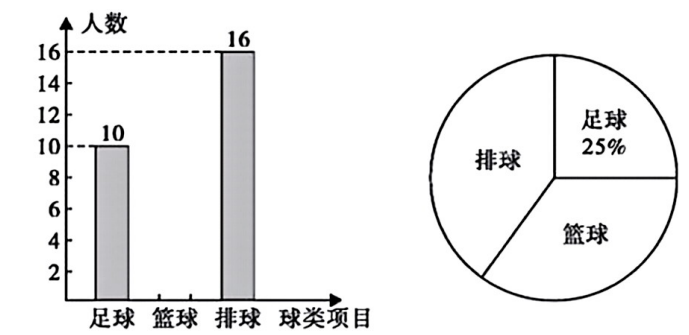
请根据图中的信息，解答下列问题：
1. （1）共调查了 ▲名学生，把条形统计图补充完整；
2. （2）求扇形统计图中“足球”对应的扇形圆心角的度数；
3. （3）该校共有1200名学生，请你估计其中最喜欢排球的学生人数.
答案解析收藏纠错 + 选题
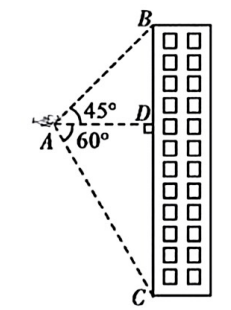
18. (2024·长沙模拟) “科技改变生活”，小王是一名摄影爱好者，新入手一台无人机用于航拍.在一次航拍时，数据显示，从无人机 $\text{[math]}$ 看建筑物顶部 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，看底部 $\text{[math]}$ 的俯角为 $\text{[math]}$ ，无人机 $\text{[math]}$ 到该建筑物BC的水平距离AD为10米，求该建筑物BC的高度.(结果精确到0.1米；参考数据： $\text{[math]}$ )

答案解析收藏纠错 + 选题
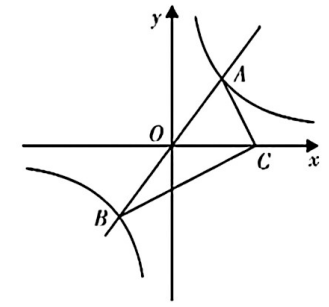
19. (2023·甘孜) 如图，在平面直角坐标系xOy中，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ 两点.
1. （1）求反比例函数的解析式；
2. （2）若点 $\text{[math]}$ 为 $\text{[math]}$ 正半轴上一点，且满足 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
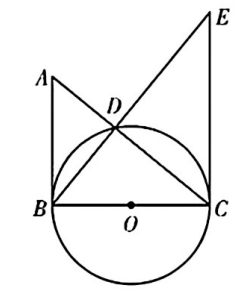
20. (2023·甘孜) 如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，以BC为直径的 $\text{[math]}$ 交AC边于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的切线，交BD的延长线于点 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的半径.
答案解析收藏纠错 + 选题

四、填空题(本大题共5个小题,每小题4分,共20分)

21. (2024九上·永定期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
22. (2023·甘孜) 一天晚上，小张帮助妈妈清洗两个只有颜色不同的有盖茶杯，突然停电了，小张只好把杯盖和茶杯随机搭配在一起.则颜色搭配正确的概率是.

答案解析收藏纠错 + 选题
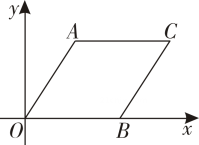
23. 如图，在平面直角坐标系 $\text{[math]}$ 中，菱形AOBC的顶点B在x轴的正半轴上，点A的坐标为 $\text{[math]}$ ，则点C的坐标为．

答案解析收藏纠错 + 选题
24. (2023·甘孜) 有一列数，记第 $\text{[math]}$ 个数为 $\text{[math]}$ ，已知 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
25. (2023·甘孜) 如图，在矩形ABCD中， $\text{[math]}$ ，点P，Q分别在AB和AC上， $\text{[math]}$ 为PQ上一点，且满足 $\text{[math]}$ .连接AM，DM，若 $\text{[math]}$ ，则AP的长为.

答案解析收藏纠错 + 选题

五、解答题(本大题共3个小题，共30分)

26. (2023·甘孜) 某次气象探测活动中，在一广场上同时释放两个探测气球.1号探测气球从距离地面5米处出发，以1米/分的速度上升，2号探测气球距离地面的高度y(单位：米)与上升时间x(单位：分)满足一次函数关系，其图象如图所示.
1. （1）求y关于 $\text{[math]}$ 的函数解析式；
2. （2）探测气球上升多长时间时，两个气球位于同一高度?此时它们距离地面多少米?
答案解析收藏纠错 + 选题
27. (2023·甘孜) 如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在AB边上，连接CD，将CD绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到CE，连接BE，DE.
1. （1）求证： $\text{[math]}$ ；
2. （2）若AD=2时，求CE的长；
3. （3）点D在AB上运动时，试探究AD²+BD²的值是否存在最小值，如果存在，求出这个最小值；如果不存在，请说明理由.
答案解析收藏纠错 + 选题
28. (2023·甘孜) 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴相交于 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ .
1. （1）求b，c的值；
2. （2） P为第一象限抛物线上一点， $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积相等，求直线AP的解析式；
3. （3）在(2)的条件下，设E是直线BC上一点，点 $\text{[math]}$ 关于AE的对称点为点 $\text{[math]}$ ，试探究，是否存在满足条件的点 $\text{[math]}$ ，使得点 $\text{[math]}$ 恰好落在直线BC上，如果存在，求出点 $\text{[math]}$ 的坐标；如果不存在，请说明理由.
答案解析收藏纠错 + 选题