浙江省杭州市拱墅区公益中学2023-2024学年九年级（上）...

更新时间：2024-09-10 浏览次数：48 类型：月考试卷

一、选择题（本大题共10小题，共30分）

1. (2024九上·拱墅月考) 抛物线y＝x²+1的顶点坐标是（）

A . （2，1） B . （0，1） C . （1，0） D . （1，2）

答案解析收藏纠错 + 选题
2. (2024九上·拱墅月考) 若 $\text{[math]}$ ＝ $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·拱墅月考) 袋子里有8个红球，m个黑球，每个球除颜色外都相同，从中任意摸出一个球，若摸到红球的可能性比摸到黑球的可能性大，则m的值不可能是（）

A . 10 B . 5 C . 3 D . 1

答案解析收藏纠错 + 选题
4. (2024九上·拱墅月考) 若某圆弧所在圆的半径为2，弧所对的圆心角为120°，则这条弧长为（）

A . $\text{[math]}$ B . π C . $\text{[math]}$ D . 2π

答案解析收藏纠错 + 选题
5. (2024九上·拱墅月考) 黄金分割由于其美学性质，受到摄影爱好者和艺术家的喜爱，摄影中有一种拍摄手法叫黄金构图法．其原理是：如图，将正方形ABCD的底边BC取中点E ，以E为圆心，线段DE为半径作圆，其与底边BC的延长线交于点F ，这样就把正方形ABCD延伸为矩形ABFG ，称其为黄金矩形．若CF＝4a ，则AB＝（　　）

A . （ $\text{[math]}$ ﹣1）a B . （2 $\text{[math]}$ ﹣2）a C . （ $\text{[math]}$ +1）a D . （2 $\text{[math]}$ +2）a

答案解析收藏纠错 + 选题
6. (2024九上·拱墅月考) 如图，在 $\text{[math]}$ 中，F是 $\text{[math]}$ 上一点， $\text{[math]}$ 交 $\text{[math]}$ 于点E， $\text{[math]}$ 的延长线交 $\text{[math]}$ 的延长线于点G， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 4 B . 6 C . 8 D . 10

答案解析收藏纠错 + 选题
7. (2024九上·拱墅月考) 若一次函数y＝（n+1）x+n的图象过第一、三、四象限，则函数y＝nx²﹣nx（　　）

A . 有最大值 $\text{[math]}$ B . 有最大值- $\text{[math]}$ C . 有最小值 $\text{[math]}$ D . 有最小值- $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·拱墅月考) 已知点A（﹣2，a﹣1），B（﹣1，a），C（1，a）在同一个函数图象上，这个函数图象可以是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2024九上·拱墅月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上的一点， $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为直径作 $\text{[math]}$ ，当 $\text{[math]}$ 与 $\text{[math]}$ 的交点落在 $\text{[math]}$ 上时， $\text{[math]}$ 的值为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
10. (2024九上·拱墅月考) 如图，在△ABC中，D是边BC上的点（不与点B ， C重合）．过点D作DE∥AB交AC于点E；过点D作DF∥AC交AB于点F、N是线段BF上的点，BN＝2NF：M是线段DE上的点，DM＝2ME ．若已知△CMN的面积，则一定能求出（　　）

A . △AFE的面积 B . △BDF的面积 C . △BCN的面积 D . △DCE的面积

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，共24分）

11. (2024九上·拱墅月考) 某工厂对一批衬衣进行抽检，随机抽取大量的衬衣后，算得合格衬衣的频率为0.9．估计在这一批衬衣中，1200件衬衣中有件是合格的．

答案解析收藏纠错 + 选题
12. (2024九上·拱墅月考) 请写出一个开口向上且经过（0，1）的抛物线的解析式．

答案解析收藏纠错 + 选题
13. (2024九上·拱墅月考) 如图， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的半径为5，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
14. (2024九上·拱墅月考) 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，CD⊥AB，垂足为D，E为BC的中点，AE与CD交于点F，则DF的长为

答案解析收藏纠错 + 选题
15. (2024九上·拱墅月考) 如图，点A、B、O是单位为1的正方形网格上的三个格点，⊙O的半径为OA ，点P是优弧 $\text{[math]}$ 的中点，则△APB的面积为．

答案解析收藏纠错 + 选题
16. (2024九上·拱墅月考) 以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt﹣4.9t² ．现将某弹性小球从地面竖直向上抛出，初速度为v₁ ，经过时间t₁落回地面，运动过程中小球的最大高度为h₁；小球落地后，竖直向上弹起，初速度为v₂ ，经过时间t₂落回地面，运动过程中小球的最大高度为h₂ ．若h₁＝1.21h₂ ，则t₁：t₂＝．

答案解析收藏纠错 + 选题

三、解答题（本大题共8大题，共66分）

17. (2024九上·拱墅月考) 如图，已知抛物线y＝﹣x²+mx+3经过点M（﹣2，3）．
1. （1）求m的值，并求出此抛物线的顶点坐标；
2. （2）当﹣3≤x≤0时，直接写出y的取值范围．
答案解析收藏纠错 + 选题
18. (2024九上·拱墅月考) 小明和小亮都想去观看“垃圾分类”宣传演出，但只有一张入场券，于是他们设计了一个“配紫色”游戏： $\text{[math]}$ ， $\text{[math]}$ 是两个可以自由转动的转盘，每个转盘都被分成面积相等的几个扇形．同时转动两个转盘，如果其中一个转盘转出了红色，另一个转盘转出了蓝色，那么可以配成紫色．若配成紫色，则小明去观看，否则小亮去观看．
1. （1）转动转盘 $\text{[math]}$ 一次，转出蓝色的概率是；
2. （2）这个游戏对双方公平吗？请说明理由（用树状图或列表法）．
答案解析收藏纠错 + 选题
19. (2024九上·拱墅月考) 如图， $\text{[math]}$ ， AB交 $\text{[math]}$ 于点C ， D ， OE是半径，且 $\text{[math]}$ 于点F ．
1. （1）求证： $\text{[math]}$ ．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
20. (2024九上·拱墅月考) 如图，在△ABC中，D是边AB上一点．
1. （1）当∠ACD＝∠B时，
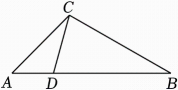
  ①求证：△ABC～△ACD；
  ②若AD＝1，BD＝3，求AC的长；
2. （2）已知 $\text{[math]}$ ，若CD＝2，求BC的长．
答案解析收藏纠错 + 选题
21. (2024九上·拱墅月考) 学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．
1. （1）小丽先调整自己的位置至点P ，将直角三角形纸板的三个顶点位置记为A、B、C（如图①），斜边AB平行于地面MN（点M、P、E、N在一直线上），且点D在边AC（较长直角边）的延长线上，此时测得边AB距离地面的高度EF为1.5米，小丽与古树的距离AF为16米，求古树的高度DE；
2. （2）为了尝试不同的思路，小丽又向前移动自己的位置至点Q ，将直角三角形纸板的三个顶点的新位置记为A^'、B^'、C^'（如图②），使直角边B^'C^'（较短直角边）平行于地面MN（点M、Q、E、N在一直线上），点D在斜边B^'A^'的延长线上，且测得此时边B^'C^'距离地面的高度依然是1.5米，那么小丽向前移动了多少米？
答案解析收藏纠错 + 选题
22. (2024九上·拱墅月考) 如图，在锐角△ABC中，AC是最短边．以AC为直径的⊙O ，交BC于D ，过O作OE∥BC ，交⊙O于E ，连接AD、AE、CE ．
1. （1）求证：∠ACE＝∠DCE；
2. （2）若∠B＝45°，∠BAE＝15°，求∠EAO的度数；
3. （3）若AC＝1， $\text{[math]}$ ，求CF的长．
答案解析收藏纠错 + 选题

23. (2024九上·拱墅月考) 根据以下素材，探索完成任务．

如何设计拱桥上救生圈的悬挂方案？

素材1

图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，过抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，如图2所示．

某时测得水面宽20m ，拱顶离水面最大距离为10m ，抛物线拱形最高点与x轴的距离为5m ．据调查，该河段水位在此基础上再涨1m达到最高．

素材2

为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m ，且相邻两救生圈悬挂点的水平间距为4m ．为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）

（1）【确定桥拱形状】根据图2，求抛物线的函数表达式．
（2）【拟定设计方案】求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
（3）【探究救生绳长度】当水位达到最高时，上游一个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数．）

答案解析收藏纠错 + 选题

24. (2024九上·拱墅月考) 如图1，四边形ABCD内接于⊙O ， BD为直径，上存在点E ，满足，连结BE并延长交CD的延长线于点F ， BE与AD交于点G ．
1. （1）若∠DBC＝α，请用含α的代数式表示∠AGB；
2. （2）如图2，连结CE ， CE＝BG ．求证：EF＝DG；
3. （3）如图3，在（2）的条件下，连结CG ， AD＝2，求CG的最小值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省杭州市拱墅区公益中学2023-2024学年九年级（上）...

副标题：

*注意事项：

浙江省杭州市拱墅区公益中学2023-2024学年九年级（上）...

试题分析

总体分析

题量分析

难度分析

知识点分析