 B .
B .  C .
C .  D .
D . 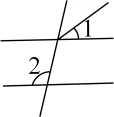
 B .
B . 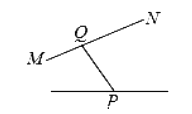 C .
C . 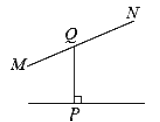 D .
D . 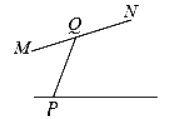
|
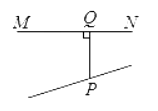
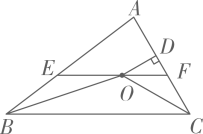
方案Ⅰ 1.作一直线EF,交AB,CD于点E,F; 2.测量∠AEF和∠CFE的大小; 3.计算180°-∠AEF-∠CFE即可. |
方案Ⅱ 1.作一直线EF,交AB,CD于点E,F; 2.摆放三角板,使两直角边恰分别过点E,F; 3.测量∠AEG和∠CFG的大小; 4.计算90°-∠AEG-∠CFG即可. |
关于方案Ⅰ、Ⅱ的可行性,下列选项正确的是( )
①同位角相等;
②在同一平面内,两条不相交的线段是平行线;
③在同一平面内,如果a//b,b//c,则a//c;
④在同一平面内,过直线外一点有且只有一条直线与已知直线平行.


如图1,AB∥CD,AP平分∠BAC,CP⊥AC,∠1是AP与AB的夹角,∠2是CP与CD的夹角,
①若∠2=22°,求∠1的度数;
②试说明:2∠1﹣∠2=90°.
解:如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).