 B .
B .  C .
C .  D .
D . 
![]()
指距d/厘米 | 20 | 21 | 22 | 23 |
身高h/厘米 | 160 | 169 | 178 | 187 |
根据如表解决下面这个实际问题:姚明的身高是226厘米,可预测他的指距约为 厘米.(结果精确到0.1)
进货单
商品 | 进价/(元/件) | 数量/件 | 金额/元 |
绩溪山核桃 | 45 |
| |
黄山毛峰 | 75 | ||
商品采购员李经理对采购情况回忆如下:两种商品共采购了100件.
①求出y与x的函数关系式;
②若李经理用不超过5000元采购这两种商品,问他最多能购买黄山毛峰多少件?

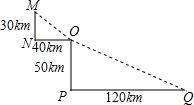
【模型应用】