 B .
B .  C .
C .  D .
D . 



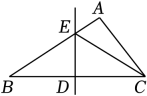


已知:如图1,直线l及直线l上一点A.
求作:△ABC,使得∠ACB=90°,∠ABC=30°.

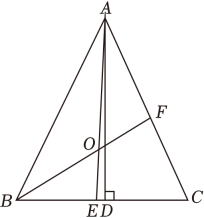
作法:如图2,
①在直线l上取点D;
②分别以点A,D为圆心,AD长为半径画弧,交于点B,E;
③作直线BE,交直线l于点C;
④连接AB.
△ABC就是所求作的三角形.
根据小明设计的尺规作图过程,
证明:连接BD,EA,ED.
∵BA=BD=AD,
∴△ABD是等边三角形.
∴∠BAD=60°.
∵BA=BD,EA= ▲ ,
∴点B,E在线段AD的垂直平分线上( )(填推理的依据).
∴BE⊥AD.
∴∠ACB=90°.
∴∠ABC+∠BAD=90°( )(填推理的依据).
∴∠ABC=30°.


(Ⅰ)A,B两种茶叶每盒进价分别为多少元?
(Ⅱ)若第一次所购茶叶全部售完后,第二次购进A,B两种茶叶共100盒(进价不变),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元,两种茶叶各售出一半后,为庆祝元旦,两种茶叶均打七折销售,全部售出后,第二次所购茶叶的利润为5800元(不考虑其他因素),求本次购进A,B两种茶叶各多少盒?
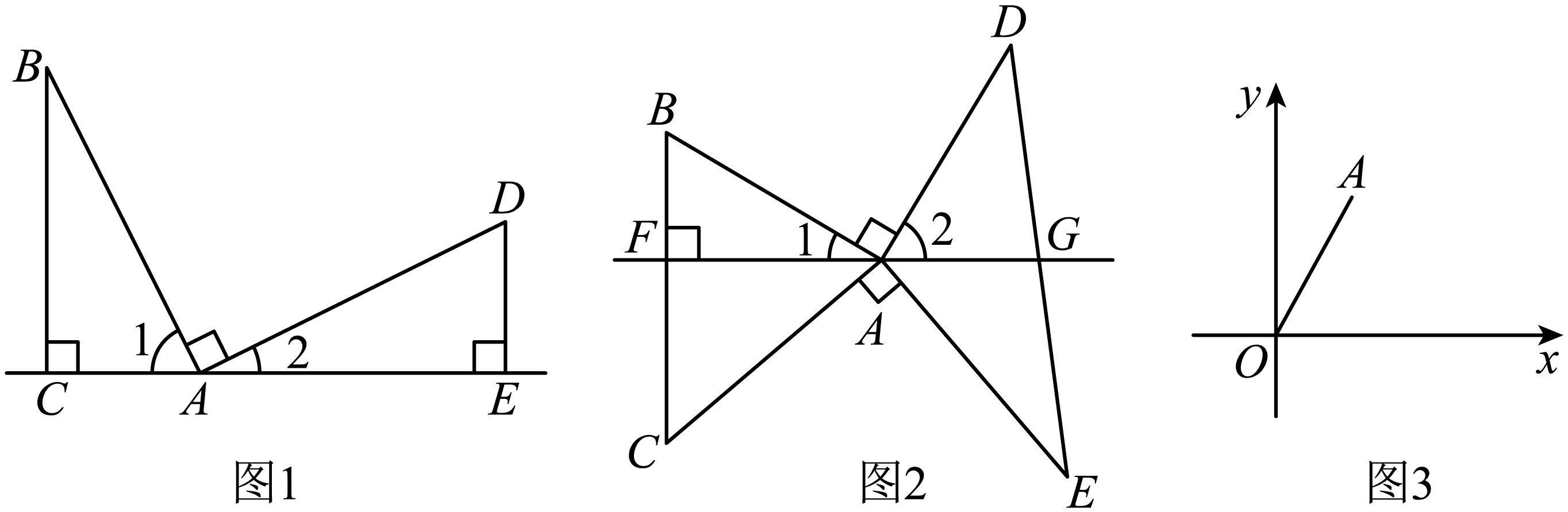
如图1, , 过点B作
于点C,过点D作
于点E.由
, 得
. 又
, 可以推理得到
. 进而得到AC=,BC=.我们把这个数学模型称为“K字”模型或“一线三等角”模型;
①如图2, , 连接
, 且
于点F,
与直线
交于点G.求证:点G是
的中点;
②如图3,在平面直角坐标系xOy中,点A的坐标为 , 点B为平面内任一点.若
是以
为斜边的等腰直角三角形,请直接写出点B的坐标.