一、选择题(本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
A . 7∶2
B . 4∶7
C . 2∶7
D . 7∶4
-
-
A .  是原来的4倍
B . 周长是原来的2倍
C . 对应边长是原来的4倍
D . 对应中线长是原来的4倍
是原来的4倍
B . 周长是原来的2倍
C . 对应边长是原来的4倍
D . 对应中线长是原来的4倍
-
4.
(2023九上·义乌月考)
在一个不透明的盒子中装有3枚仅有颜色不同的棋子,其中1枚白色棋子和2枚黑色棋子.从中随机摸出一枚棋子,记录其颜色后放回,再从盒子中随机摸出一枚棋子,记录其颜色,则两次记录的颜色不同的概率是( )
-
A . 函数图象的对称轴为直线 B . 函数的最大值为2
C . 当
B . 函数的最大值为2
C . 当 时,
时, 随
随 的增大而增大
D . 函数图象与
的增大而增大
D . 函数图象与 轴的交点坐标为
轴的交点坐标为
-
6.
(2023九上·义乌月考)
筒车是我国古代发明的一种水利灌溉工具.如图,筒车盛水桶的运行轨道是以轴心

为圆心的圆,已知圆心

在水面上方,且圆

被水面截得的弦AB长为6米,半径长为4米.若点

为运行轨道的最低点,则点

到AB的距离等于( )

A . 1米
B .  米
C . 2米
D .
米
C . 2米
D .  米
米
-
7.
(2023九上·义乌月考)
定义:如果两个锐角的和为

, 那么称这两个角互为半余角.如图,在

中,

互为半余角,且

, 则

( )

-
8.
(2023九上·义乌月考)
如图,点

在线段BD上,在BD的同侧作等腰三角形ABC和等腰三角形

,

分别与CD,AC交于点P,M.设

, 下列结论一定正确的是( )

-
9.
(2023九上·义乌月考)
将三角形纸片ABC按如图所示的方式折叠,使点

落在边AC上的点

处,折痕为EF.已知

, 若以点

为顶点的三角形与

相似,则

( )

-
二、填空题(本大题有6个小题,每小题4分,共24分)
-
-
12.
(2023九上·义乌月考)
一名男生在一个水平的训练场地里推铅球,铅球飞行高度

与距离该男生的水平距离

之间满足:

, 则铅球推出的距离为
m.
-
13.
(2023九上·义乌月考)
如图,一张纸片上有一个不规则的图案(图中的小兔子),小雅想知道该图案的面积是多少,她采取了以下的办法:用一个长为

, 宽为

的长方形将该图案围起来,然后在适当位置随机地向长方形区域内掷点,通过大量重复试验,发现点落在图案部分的频率稳定在0.6左右,由此她估计此不规则图案的面积大约为

.

-
-
15.
(2023九上·义乌月考)
如图,在Rt

中,

, 按以下步骤作图:①以点

为圆心,以任意长为半径作弧,分别交AC,AB于点M,N②分别以M,N为圆心,以大于

的长为半径作弧,两弧在

内交于点

;(3)作射线AO,交BC于点

.若

, 则AB的长为
.

-
16.
(2023九上·义乌月考)
如图是我国汉代的赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形EFGH组成的一个大正方形ABCD.设图中

, 连结AE,BE,若

与

的面积相等,则

.

三、解答题(本大题有8个小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)
-
-
-
(2)
若将此扇形围成一个圆锥的侧面(不计接缝),求圆锥的底面半径.
-
18.
(2023九上·义乌月考)
杭州第19届亚运会有三个重要的竞赛场馆,分别为:A.大莲花奥体中心,B.黄龙体育中心,C.化蝶游泳馆.小明和小颖都是志愿者,他们被随机分配到这三个竞赛场馆中的任意一个场馆的可能性相同.
-
(1)
小明被分配到A(大莲花奥体中心)做志愿者的概率是多少?
-
(2)
利用画树状图或列表的方法,求小明和小颖都被分配到B(黄龙体育中心)做志愿者的概率.
-
19.
(2023九上·义乌月考)
数学实践活动:901班测量校园小山坡护坡石坝的有关数据 |
活动1 | 如图1,测角小组用一根木条EF斜靠在护坡石坝上,使得BF与BE的长度相等,如果测量得到∠EFB=30°,那么石坝与地面的倾角∠α的度数是▲. | 
|
活动2 | 如图2,测高小组把一根长为4米的竹竿AG斜靠在石坝旁(A点在石坝顶部,G点在地面),量出竿长GM=1米时离地面的高度为0.5米,请你求出护坡石坝的垂直高度AH. | 
|
实践活动总结归纳 |
大家总结各组的方法后,设计了如图3方案:在护坡石坝顶部的影子处立一根长为a米的杆子PD,杆子与地面垂直,测得杆子的影子长为b米,点P到护坡石坝底部B的距离为c米.利用测角小组得到的倾角∠α的度数,请你用a,b,c表示出护坡石坝的垂直高度AH. | 
|
-
-
21.
(2023九上·义乌月考)
在同一平面直角坐标系中,若函数

与

的图象只有一个公共点,则称

是

的相切函数,公共点称为切点.已知函数

, 且

是

的相切函数,

为切点.
-
-
(2)
当m,n分别取以下两组值时,①m=2,n=-2;②m=-3,n=3,不等式

是否成立?说明理由.
-
22.
(2023九上·义乌月考)
如图是一座拱桥的截面图,拱桥桥洞的形状是抛物线.平时水面的宽度OA为4m,在离水面高1.5m处,有一条航运船舶限高杠杆PD,杠杆PD长2m.以O为原点,OA所在直线为x轴建立如图所示的直角坐标系.

-
-
(2)
因为上游水库泄洪,水面上涨了0.5m,则此时水面的宽度是多少?

, 结果精确到

-
-
24.
(2023九上·义乌月考)
如图,在

中,

是

的外接圆,连结BO并延长交

于点

, 连结AD,CD.在

上取一点

, 使

, 连结BF,CF,BF与AC交于点

.

-
(1)
试求

与
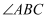
的数量关系.
-
(2)
求证:

.
-
(3)
已知

的半径为2,若

,
①试判断 的形状;②求
的形状;②求 的面积.
的面积.








在AB边上,点
在对角线AC上,
, 求证:
.
, 点
在AB边上,点
在对角线AC上,
, 求CF的长
, 点
在AB边上,点
在对角线AC上,
, 作
交DA的延长线于点H,DE的延长线交BH于点
, 请直接写出BP,BE的长.
的形状;②求
的面积.