题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

湖南省常德市初中教学联盟校2023-2024学年九年级上学期...

更新时间：2024-05-22 浏览次数：41 类型：期末考试

一、选择题（本大题共8小题，每小题3分，共24分）

1. (2023九上·武侯月考) 下列是关于 $\text{[math]}$ 的一元二次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·巫山县期末) 某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验，得到两个品种每公顷产量的两组数据，其方差分别为s_甲²=0.002、s_乙²=0.03，则（　　）

A . 甲比乙的产量稳定 B . 乙比甲的产量稳定 C . 甲、乙的产量一样稳定 D . 无法确定哪一品种的产量更稳定

答案解析收藏纠错 + 选题
3. (2024九上·常德期末) 若∠A为锐角，且sinA＝ $\text{[math]}$ ，则cosA的值是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·常德期末) 线段 $\text{[math]}$ ， P是AB的黄金分割点，且 $\text{[math]}$ ，则BP的长度为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·常德期末) 怎样移动抛物线 $\text{[math]}$ 就可以得到抛物线 $\text{[math]}$ （）

A . 左移1个单位、上移2个单位 B . 左移1个单位、下移2个单位 C . 右移1个单位、上移2个单位 D . 右移1个单位、下移2个单位

答案解析收藏纠错 + 选题
6. (2024九上·常德期末) 如图，河堤的横断面迎水坡 $\text{[math]}$ 的坡比是 $\text{[math]}$ ，堤高 $\text{[math]}$ ，则坡面 $\text{[math]}$ 的长度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九上·常德期末) 如图所示，由四个全等的直角三角形围成的大正方形的面积是169，小正方形的面积为49，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·常德期末) 定义：在平面直角坐标系中，若点A满足横、纵坐标都为整数，则把点A叫做“整点”．如：B（3，0）、C（﹣1，3）都是“整点”．抛物线y＝ax²﹣2ax+a+2（a＜0）与x轴交于点M，N两点，若该抛物线在M、N之间的部分与线段MN所围的区域（包括边界）恰有5个整点，则a的取值范围是（　　）

A . ﹣1≤a＜0 B . ﹣2≤a＜﹣1 C . ﹣1≤a＜ $\text{[math]}$ D . ﹣2≤a＜0

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，每小题3分，共24分）

9. (2024九上·常德期末) 如图，Rt△ABC中， $\text{[math]}$ ， AC＝5，BC＝12，则cosA的值为．

答案解析收藏纠错 + 选题
10. (2024九上·常德期末) 已知 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
11. (2024九上·常德期末) 如图， $\text{[math]}$ ，直线l₁、l₂与这三条平行线分别交于点A、B、C和点D、E、F．若 $\text{[math]}$ ， $\text{[math]}$ ，则DF的长为．

答案解析收藏纠错 + 选题
12. (2024九上·常德期末) 在平面直角坐标系中， $\text{[math]}$ 和 $\text{[math]}$ 的相似比等于 $\text{[math]}$ ，并且是关于原点 $\text{[math]}$ 的位似图形，若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则其对应点 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题
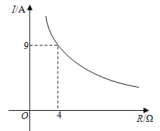
13. (2024九上·常德期末) 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．若蓄电池电流为3A时，电阻为Ω．

答案解析收藏纠错 + 选题
14. (2024九上·常德期末) 若点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都在反比例函数 $\text{[math]}$ （K为常数）的图象上，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的大小关系为．

答案解析收藏纠错 + 选题
15. (2024九上·常德期末) 如图，在△ABC中，点D，E分别在AB，AC上，∠AED＝∠B， $\text{[math]}$ ，若四边形BCED的面积为7，则△ADE的面积为.

答案解析收藏纠错 + 选题
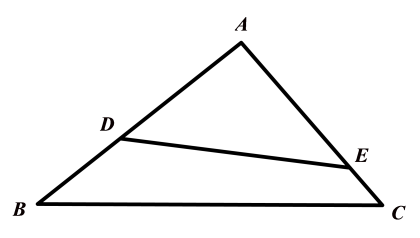
16. (2024九上·常德期末) 如上图，在平面直角坐标系中，正方形 $\text{[math]}$ 与正方形 $\text{[math]}$ 是以原点为位似中心的位似图形，且相似比为 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 轴上，延长 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ；延长 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ …，若 $\text{[math]}$ ，则正方形 $\text{[math]}$ 的面积是．

答案解析收藏纠错 + 选题

三、解答题（本大题共2小题，每小题5分，共10分）

17. (2024九上·常德期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2024九上·常德期末) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题

四、解答题（本大题共2小题，每小题6分，共12分）

19. (2024九上·扶绥期末) 如图，在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ，且 $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024九上·常德期末) 已知关于x的一元二次方程 $\text{[math]}$ 有实数根.
1. （1）求m的取值范围；
2. （2）如果方程的两个实数根为 $\text{[math]}$ 、 $\text{[math]}$ ，且 $\text{[math]}$ ，求m的取值范围.
答案解析收藏纠错 + 选题

五、解答题（本大题共2小题，每小题7分，共14分）

21. (2024九上·常德期末) 某学校为了进一步丰富学生的体育活动，欲增购一些体育器材，为此对该校一部分学生进行了一次“你最喜欢的体育活动”的问卷调查（每人只选一项）．根据收集到的数据绘制成如下统计图（不完整）：请根据图中提供的信息完成下列问题：
1. （1）在这次问卷调查中，一共抽查了 ▲ 名学生，并在图中补全条形统计图。
2. （2）如果全校有3600名学生，那么全校学生中最喜欢“踢毽”活动的学生约有多少人？
答案解析收藏纠错 + 选题
22. (2024九上·常德期末) 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图像交于 $\text{[math]}$ ， $\text{[math]}$ 两点．
1. （1）求一次函数表达式和反比例函数表达式；
2. （2）直接写出关于x的不等式 $\text{[math]}$ 的解集；
3. （3）求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题

六、解答题（本大题共2小题，每小题8分，共16分）

23. (2024九上·常德期末) 2023年杭州亚运会胜利闭幕，本次亚运会中国代表团共获得383枚奖牌，位居奖牌榜第一位，创造了新的历史。在亚运会期间，买一件印有亚运会元素的T恤去看比赛，成为了体育迷们的“仪式感”。商店以40元每件的价格购进一批这样的T恤，以每件60元的价格出售。经统计，四月份的销售量为192件，六月份的销售量为300件。
1. （1）求该款T恤四月份到六月份销售量的月平均增长率。
2. （2）从七月份起，商场决定采用降价销售回馈顾客，经试验，发现该款T恤在六月销售量的基础上，每降1元，月销售量就会增加20件。如何定价才能使利润最大？
答案解析收藏纠错 + 选题
24. (2024九上·常德期末) “五一”节期间，许多露营爱好者在我市郊区露营，为遮阳和防雨会搭建一种“天幕”，其截面示意图是轴对称图形，如图，对称轴垂直于地面的支杆 $\text{[math]}$ 所在直线，用绳子拉直 $\text{[math]}$ 后系在树干 $\text{[math]}$ 上的点E处，使得点A、D、E在一条直线上，通过调节点E的高度可控制“天幕”的开合， $\text{[math]}$ ．
（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）天晴时打开“天幕”，若 $\text{[math]}$ ，求遮阳宽度 $\text{[math]}$ （结果精确到0.1m）；
2. （2）下雨时收拢“天幕”， $\text{[math]}$ 从 $\text{[math]}$ 减少到 $\text{[math]}$ ，求点E下降的高度．（结果精确到0.1m）．
答案解析收藏纠错 + 选题

七、解答题（本大题共2小题，每小题10分，共20分）

25. (2024九上·常德期末) 综合与实践
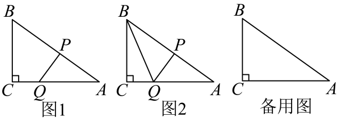
如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点P以每秒2个单位长度的速度从点A出发，沿 $\text{[math]}$ 方向向终点B匀速运动，同时点Q以每秒1个单位长度的速度从点C出发，沿 $\text{[math]}$ 方向向终点A匀速运动，连接 $\text{[math]}$ ．设运动的时间为t秒．
1. （1）求 $\text{[math]}$ 的长（用含t的代数式表示）．
2. （2）当 $\text{[math]}$ 秒时，求 $\text{[math]}$ 的面积．
3. （3）如图2，连接 $\text{[math]}$ ，当 $\text{[math]}$ 为直角三角形时，求所有满足条件t的值．
答案解析收藏纠错 + 选题
26. (2024九上·常德期末) 如图1，在平面直角坐标中，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ 、 $\text{[math]}$ 两点，与y轴交于点C ，连接 $\text{[math]}$ ，直线 $\text{[math]}$ 交y轴于点M ． P为直线 $\text{[math]}$ 上方抛物线上一动点，过点P作x轴的垂线，分别交直线 $\text{[math]}$ 、 $\text{[math]}$ 于点E、F ．
1. （1）求抛物线的表达式；
2. （2）当点P落在抛物线的对称轴上时，求 $\text{[math]}$ 的面积；
3. （3）若点N为y轴上一动点，当四边形 $\text{[math]}$ 为矩形时，求点N的坐标；
答案解析收藏纠错 + 选题

试卷信息