2024年江西省初中学业水平考试数学模拟卷（一）

更新时间：2024-03-19 浏览次数：104 类型：中考模拟

一、选择题（本大题共6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的）

1. (2023·陕西) 计算： $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·青岛) 生活中有许多对称美的图形，下列是中心对称图形但不是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·西宁) 下列说法正确的是（）

A . 检测“神舟十六号”载人飞船零件的质量，应采用抽样调查 B . 任意画一个三角形，其外角和是180°是必然事件 C . 数据4，9，5，7的中位数是6 D . 甲、乙两组数据的方差分别是 $\text{[math]}$ ， $\text{[math]}$ ，则乙组数据比甲组数据稳定

答案解析收藏纠错 + 选题
4. (2023·镇江) 下列运算中，结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·丹东) 如图，直线 $\text{[math]}$ 过点 $\text{[math]}$ ， $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·娄底) 我国南宋著名数学家秦九韶在他的著作《数学九章》一书中，给出了这样的一个结论：三边分别为a、b、c的 $\text{[math]}$ 的面积为 $\text{[math]}$ ． $\text{[math]}$ 的边a、b、c所对的角分别是∠A、∠B、∠C，则 $\text{[math]}$ ．下列结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题，共15.0分）

7. (2020·历下模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
8. (2023·灯塔模拟) 《全国防沙治沙规划（ $\text{[math]}$ 年》》正式印发实施，提出到2030年，规划完成沙化土地治理任务1.86亿亩．数据“1.86亿”用科学记数法表示为．

答案解析收藏纠错 + 选题
9. (2023·西宁) 有五张看上去无差别的卡片，正面分别写着 $\text{[math]}$ ， $\text{[math]}$ ， -0.5， $\text{[math]}$ ， 0.背面朝上混合后随机抽取一张，取出的卡片正面的数字是无理数的概率是.

答案解析收藏纠错 + 选题
10. (2023·益阳) 如图，正六边形 $\text{[math]}$ 中， $\text{[math]}$ °．

答案解析收藏纠错 + 选题
11. (2023·丹东) 如图，点 $\text{[math]}$ 是反比例函数 $\text{[math]}$ 的图象上一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，垂足为点 $\text{[math]}$ ，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 轴上任意一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 的面积是 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2023·济南) 如图，将菱形纸片 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线折叠，使点 $\text{[math]}$ 落在射线 $\text{[math]}$ 上的点 $\text{[math]}$ 处，折痕 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长等于．

答案解析收藏纠错 + 选题

三、解答题（一）

13. (2023·新余模拟)
1. （1）计算： $\text{[math]}$ ．
2. （2）如图，在平行四边形 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且四边形 $\text{[math]}$ 为正方形 $\text{[math]}$ 求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
14. (2023·淄博) 若实数 $\text{[math]}$ ， $\text{[math]}$ 分别满足下列条件：
$\text{[math]}$ ；（2） $\text{[math]}$ ．试判断点 $\text{[math]}$ 所在的象限

答案解析收藏纠错 + 选题
15. (2023·青岛) 用直尺、圆规作图，不写作法，但要保留作图痕迹．
已知： $\text{[math]}$ ．
求作：点P ，使 $\text{[math]}$ ，且点P在 $\text{[math]}$ 边 $\text{[math]}$ 的高上．

答案解析收藏纠错 + 选题
16. (2023·广州) 甲、乙两位同学相约打乒乓球．
1. （1）有款式完全相同的4个乒乓球拍 $\text{[math]}$ 分别记为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若甲先从中随机选取1个，乙再从余下的球拍中随机选取1个，求乙选中球拍C的概率；
2. （2）双方约定：两人各投掷一枚质地均匀的硬币，如果两枚硬币全部正面向上或全部反面向上，那么甲先发球，否则乙先发球 $\text{[math]}$ 这个约定是否公平？为什么？
答案解析收藏纠错 + 选题
17. (2019·白银) 如图，已知反比例函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象在第一象限交于 $\text{[math]}$ 两点
1. （1）求反比例函数和一次函数的表达式；
2. （2）已知点 $\text{[math]}$ ，过点 $\text{[math]}$ 作平行于 $\text{[math]}$ 轴的直线，在第一象限内交一次函数 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，交反比例函数 $\text{[math]}$ 上的图象于点 $\text{[math]}$ .若 $\text{[math]}$ ，结合函数图象直接写出 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题

四、解答题（二）

18. (2023·陕西) 小华想利用所学知识测量自家对面的两栋楼 $\text{[math]}$ 与 $\text{[math]}$ 的高度差 $\text{[math]}$ 如图所示，她站在自家阳台上发现，在阳台的点 $\text{[math]}$ 处恰好可经过楼 $\text{[math]}$ 的顶端 $\text{[math]}$ 看到楼 $\text{[math]}$ 的底端 $\text{[math]}$ ，即点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上 $\text{[math]}$ 此时，测得点 $\text{[math]}$ 的俯角 $\text{[math]}$ ，点 $\text{[math]}$ 的仰角 $\text{[math]}$ ，并测得 $\text{[math]}$ ， $\text{[math]}$ 已知， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一水平直线上 $\text{[math]}$ 求楼 $\text{[math]}$ 与 $\text{[math]}$ 的高度差 $\text{[math]}$ 参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2022·铜仁) 为实施“乡村振兴”计划，某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收，销售前对本地市场进行调查发现：当批发价为4千元/吨时，每天可售出12吨，每吨涨1千元，每天销量将减少2吨，据测算，每吨平均投入成本2千元，为了抢占市场，薄利多销，该村产业合作社决定，批发价每吨不低于4千元，不高于5.5千元.请解答以下问题：
1. （1）求每天销量y（吨）与批发价x（千元/吨）之间的函数关系式，并直接写出自变量x的取值范围；
2. （2）当批发价定为多少时，每天所获利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
20. (2023·西宁) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的弦，半径 $\text{[math]}$ ，垂足为D ，弦 $\text{[math]}$ 与 $\text{[math]}$ 交于点F ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题

五、解答题（三）

21. (2023·益阳) 我市教育局为深入贯彻落实立德树人根本任务，2022年在全市中小学部署开展“六个一”德育行动．某校为了更好地开展此项活动，随机抽取部分学生对学校前段时间开展活动的情况进行了满意度调查，满意度分为四个等级：A：非常满意；B：满意；C：一般；D：不满意．根据调查数据绘制了如下两幅不完整的统计图表：

等级

人数

A

72

B

108

C

48

D

m

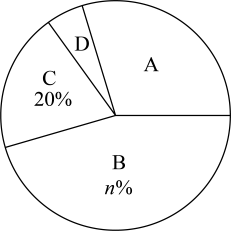
请你根据图表中的信息，解答下列问题：
1. （1）本次被调查的学生人数是多少？
2. （2）求以上图表中m ， n的值及扇形统计图中A等级对应的圆心角度数；
3. （3）若该校共有学生1200人，估计满意度为A ， B等级的学生共有多少人？
答案解析收藏纠错 + 选题
22. (2023·丹东) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点 $\text{[math]}$ 四边形 $\text{[math]}$ 是菱形 $\text{[math]}$ 按逆时针顺序排列 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，菱形 $\text{[math]}$ 可以绕点 $\text{[math]}$ 旋转，连接 $\text{[math]}$ 和 $\text{[math]}$ ，设直线 $\text{[math]}$ 和直线 $\text{[math]}$ 所夹的锐角为 $\text{[math]}$ ．
1. （1）在菱形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转的过程中，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，如图 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系及 $\text{[math]}$ 的值；
2. （2）当菱形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转到如图 $\text{[math]}$ 所示的位置时， $\text{[math]}$ 中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由；
3. （3）设直线 $\text{[math]}$ 与直线 $\text{[math]}$ 的交点为 $\text{[math]}$ ，在菱形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转一周的过程中，当 $\text{[math]}$ 所在的直线经过点 $\text{[math]}$ 时，请直接写出 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题

六、解答题（四）

23. (2023·新余模拟) 定义：在平面直角坐标系中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴的交点坐标为 $\text{[math]}$ ，那么我们把经过点 $\text{[math]}$ 且平行于 $\text{[math]}$ 轴的直线称为这条抛物线的极限分割线．
1. （1）【特例感知】
  抛物线 $\text{[math]}$ 的极限分割线与这条抛物线的交点坐标为．
2. （2）【深入探究】
  经过点 $\text{[math]}$ 和 $\text{[math]}$ 的抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，它的极限分割线与该抛物线另一个交点为 $\text{[math]}$ ，请用含 $\text{[math]}$ 的代数式表示点 $\text{[math]}$ 的坐标．
3. （3）【拓展运用】
  在（2）的条件下，设抛物线 $\text{[math]}$ 的顶点为 $\text{[math]}$ ，直线 $\text{[math]}$ 垂直平分 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，交该抛物线的对称轴于点 $\text{[math]}$ ．
  
  ①当 $\text{[math]}$ 时，求点 $\text{[math]}$ 的坐标．
  
  ②若直线 $\text{[math]}$ 与直线 $\text{[math]}$ 关于极限分割线对称，是否存在使点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离与点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离相等的 $\text{[math]}$ 的值？若存在，直接写出 $\text{[math]}$ 的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题