2023-2024学年湘教版初中数学八年级下学期 5.2 频...

更新时间：2024-03-27 浏览次数：27 类型：同步测试

一、选择题

1. 在频数直方图中有 11个小长方形，若中间一个小长方形的面积等于其他 10个小长方形面积的和的一半，且数据总数为96，则中间一组的频数为（）

A . 32 B . 0.5 C . 48 D . 0.33

答案解析收藏纠错 + 选题
2. 对某校600名学生的体重（kg）进行统计，得到如图所示的统计图（横轴上每组数据包含最小值不包含最大值），则学生体重在60kg及以上的人数为（）

A . 120 B . 150 C . 180 D . 330

答案解析收藏纠错 + 选题
3. 观察如图所示的频数直方图，其中组界为99.5~124.5这一组的频数是（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
4. 小明同学对部分菲尔兹奖得主获奖时的年龄进行了统计，得到的频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，其中获奖时年龄在36岁及以上的有（）

A . 13人 B . 27人 C . 33人 D . 47人

答案解析收藏纠错 + 选题
5. 小杰调查了本班同学的体重情况，并绘制成了频数直方图，下列结论中，错误的是（）

A . 全班总人数为45 B . 体重在50~55kg的人数最多 C . 全班学生中体重最大的是65kg D . 体重在60~65kg的人数占全班总人数的 $\text{[math]}$

答案解析收藏纠错 + 选题
6. 某次考试中，某班的数学成绩统计图如图所示，下列说法错误的是（）

A . 得分在70~80分之间的人数最多 B . 该班的总人数为40 C . 得分在90~100分之间的人数最少 D . 不及格(<60分)人数是6

答案解析收藏纠错 + 选题
7. (2023八下·茶陵期末) 小文同学统计了他所在小区居民每天微信阅读的时间，并绘制了直方图．①小文同学一共统计了60人；②每天微信阅读不足20分钟的人数有12人；③每天微信阅读30-40分钟的人数最多；④每天微信阅读0-10分钟的人数最少．根据图中信息，上述说法中正确的是（　　）

A . ①②③④ B . ①②③ C . ②③④ D . ③④

答案解析收藏纠错 + 选题
8. (2023七下·邕宁期末) 某次考试中，某班级的数学成绩统计图如下，下列说法错误的是（）

A . 得分在90~100分之间的人数最少 B . 该班的总人数为40 C . 及格（≥60分）人数是26 D . 得分在70~80分之间的人数最多

答案解析收藏纠错 + 选题

二、填空题

9. 为了解某校1000名学生在进行家务劳动时对家用燃气设备安全知识的掌握情况，随机抽取100名学生参加问卷测试，将成绩进行整理得到频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，则该校成绩为 80分及以上的学生约有人.

答案解析收藏纠错 + 选题
10. 某养殖场对200头牲畜的质量进行统计，得到频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，其中质量在77.5kg及以上的牲畜有头.

答案解析收藏纠错 + 选题
11. (2023九上·龙湾开学考) 某校对 $\text{[math]}$ 名八年级学生身高进行统计，得到频数分布直方图 $\text{[math]}$ 每一组含前一个边界值，不含后一个边界值 $\text{[math]}$ 如图所示，其中身高在 $\text{[math]}$ 及以上的学生有人 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023八上·义乌开学考) 某校学生“亚运知识”竞赛成绩的频数分布直方图 $\text{[math]}$ 每一组含前一个边界值，不含后一个边界值 $\text{[math]}$ 如图所示，其中成绩在 $\text{[math]}$ 分及以上的学生有人 $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2023八下·石景山期末) 根据某班40名学生身高的频数分布直方图（每组不含起点值，含终点值），回答下列问题：
1. （1）人数最多的身高范围是；
2. （2）身高大于175cm的学生占全班人数的百分比是．
答案解析收藏纠错 + 选题

三、解答题

14. 在太空种子种植体验实践活动中，为了解“字番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x (单位：个)，并绘制如下不完整的统计图表：
“字番2号”番茄挂果数量统计表
挂果数量x(个)
频数(株)
频率
25≤x<35
6
0.1
35≤x<45
12
0.2
45≤x<55
a
0.25
55≤x<65
18
b
65≤x<75
9
0.15
请结合图表中的信息解答下列问题：
1. （1）统计表中，a=，b=
2. （2）将频数分布直方图补充完整．
3. （3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x<45”所对应扇形的圆心角度数为°
4. （4）若所种植的“字番2号”番茄有1000株，则可以估计挂果数量在“55≤x<65"范围的番茄有株．
答案解析收藏纠错 + 选题
15. 第33届夏季奥林匹克运动会定于2024年7月26日在巴黎举行，某校七、八年级各有500名学生，为了解这两个年级学生对本次奥运会的关注程度，现从这两个年级各随机抽取n名学生进行奥运会知识测试，将测试成绩按以下六组进行整理（得分用x表示）：
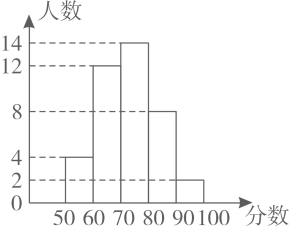
A：70≤x<75，B：75≤x<80，C：80≤x<85，
D：85<x<90， E：90≤x<95 ，F：95≤x<100.
根据得到的数据绘制七年级测试成绩频数直方图
和八年级测试成绩扇形统计图如图所示.
已知八年级测试成绩 D组的全部数据如下：
86，85，87，86，85，89，88.
请根据以上信息，完成下列问题：
1. （1） n=，a=.
2. （2）若测试成绩不低于 90分，则认定该学生对奥运会关注程度高，请估计该校七、八两个年级对奥运会关注程度高的学生总数.
答案解析收藏纠错 + 选题

四、综合题

16. (2023七下·杭州期末) 为迎接杭州亚运会的召开，某校决定在全校范围内开展亚运知识的宣传教育活动 $\text{[math]}$ 为了了解宣传效果，随机抽取部分学生，并在活动前、后对这些学生进行了两次跟踪测评，两次测评中所有同学的成绩没有低于 $\text{[math]}$ 分，现在将收集的数据制成频数分布直方图 $\text{[math]}$ 每一组包含左端值，不包含右端值 $\text{[math]}$ 和频数表 $\text{[math]}$ 宣传活动后亚运知识成绩频数表：

成绩	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
频数	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

（1）本次活动共抽取学生；
（2）宣传活动前，在抽取的学生中成绩人数最多一组的组中值是分；
（3）表中的 $\text{[math]}$ ，宣传活动后，在抽取的学生中分数高于 $\text{[math]}$ 分的至少有人，至多有人；
（4）小聪认为，宣传活动后成绩在 $\text{[math]}$ 的人数为 $\text{[math]}$ ，比活动前减少了 $\text{[math]}$ 人，因此学校开展的宣传活动没有效果 $\text{[math]}$ 请你结合统计图表，说一说小聪的看法是否正确 $\text{[math]}$ 为什么？

答案解析收藏纠错 + 选题

17. (2023·潍坊) 某中学积极推进校园文学创作，倡导每名学生每学期向校报编辑部至少投1篇稿件．学期末，学校对七、八年级的学生投稿情况进行调查．
【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生，统计每人在本学期投稿的篇数，制作了频数分布表．
投稿篇数（篇）
1
2
3
4
5
七年级频数（人）
7
10
15
12
6
八年级频数（人）
2
10
13
21
4
【数据的描述与分析】
1. （1）求扇形统计图中圆心角 $\text{[math]}$ 的度数，并补全频数直方图．
2. （2）根据频数分布表分别计算有关统计量：
  统计量
  中位数
  众数
  平均数
  方差
  七年级
  3
  3
  $\text{[math]}$
  1.48
  八年级
  m
  n
  3.3
  1.01
  直接写出表格中m、n的值，并求出 $\text{[math]}$ ．
3. （3）【数据的应用与评价】
  从中位数、众数、平均数、方差中，任选两个统计量，对七、八年级学生的投稿情况进行比较，并做出评价．
答案解析收藏纠错 + 选题