2023-2024学年冀教版初中数学八年级下册 22.1 平...

更新时间：2024-04-02 浏览次数：8 类型：同步测试

一、选择题

1. 如图，在▱ABCD中，CD=10，∠ABC的平分线交AD于点E，过点A作AF⊥BE，垂足为F.若AF=6，则BE的长为（）

A . 8 B . 10 C . 16 D . 18

答案解析收藏纠错 + 选题
2. 如图，在▱ABCD中，BE⊥CD，BF⊥AD，∠EBF=45°.若CE=3，DF=1，则▱ABCD的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 如图，过▱ABCD对角线的交点O 的直线交AD 于点E，交 BC 于点F.若▱ABCD的周长为 18，OE=1.5，则四边形 EFCD的周长为（）

A . 14 B . 13 C . 12 D . 10

答案解析收藏纠错 + 选题
4. (2024九上·交城期中) 如图，将△ABC绕点A逆时针旋转得到△ADE，连接CE，四边形ACED是平行四边形，若∠ACB=30°，则∠AEC的度数为（）

A . 45° B . 60° C . 75° D . 90°

答案解析收藏纠错 + 选题
5. (2023九上·成都月考) 如图，已知 $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ ，以点 $\text{[math]}$ 为中心，取旋转角等于 $\text{[math]}$ ，把 $\text{[math]}$ 顺时针旋转，得到 $\text{[math]}$ ，连接 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·长春期末) 如图，在▱ABCD中，AE平分∠DAB交CD于点E，AB＝7，BC＝4，则CE的长度为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
7. (2023八下·高陵期末) 如图，点O是 $\text{[math]}$ 的对角线的交点， $\text{[math]}$ ，点E、F分别是OC、OD的中点，连接BE，过点F作 $\text{[math]}$ 交边AB于点P，连接PE，则下列结论中不一定正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022八下·乐清期中) 将一副三角尺如图拼接：含30°角的三角尺（ $\text{[math]}$ ）的长直角边与含45°角的三角尺（ $\text{[math]}$ ）的斜边恰好重合.点E，F分别是边 $\text{[math]}$ ， $\text{[math]}$ 上的动点，各自同时从点A，点B向终点C运动，已知点E的速度为1单位/秒，若存在某个时刻四边形 $\text{[math]}$ 为平行四边形，则点F的速度为（）单位/秒.

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题

二、填空题

9. 如图，在▱ABCD 中，已知 $\text{[math]}$ ， AC⊥BC，则 BD=cm.

答案解析收藏纠错 + 选题
10. (2023九下·松原月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， AC为对角线，将 $\text{[math]}$ 绕点A顺时针旋转一定的角度后得到 $\text{[math]}$ ，使点D的对应点E落在边AB上，若点C的对应点F落在边CB的延长线上，则 $\text{[math]}$ 度.

答案解析收藏纠错 + 选题
11. (2022九上·温州开学考) 如图，纸片▱ABCD面积为6，AB＝3，∠BAD＝45°，按下列步骤进行裁剪和拼图．
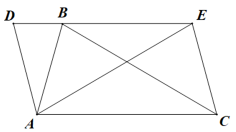
第一步：如图①，将平行四边形纸片沿对角线BD剪开，得到△ABD和△BCD纸片，再将△ABD纸片沿AE剪开（E为BD上任意一点），得到△ABE和△ADE纸片；
第二步：如图②，将△ABE纸片平移至△DCF处，将△ADE纸片平移至△BCG处；
第三步：如图③，将△DCF纸片翻转过来使其背面朝上置于△PQM处（边PQ与DC重合，△PQM和△DCF在DC同侧），将△BCG纸片翻转过来使其背面朝上置于△PRN处，（边PR与BC重合，△PRN和△BCG在BC同侧）．
由此可知，由纸片拼成的五边形PMQRN中，对角线MN长度的最小值为．

答案解析收藏纠错 + 选题
12. 如图，在▱ABCD中，对角线 AC，BD 相交于点O，E为BC 的中点，F，G为边CD 上的点，且 FG $\text{[math]}$ 连结OF，EG.若▱ABCD的面积为 60，则图中阴影部分的面积是.

答案解析收藏纠错 + 选题
13. (2023·黄石) 如图，将▱ $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转到▱ $\text{[math]}$ 的位置，使点 $\text{[math]}$ 落在 $\text{[math]}$ 上， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ 从“ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ”中选择一个符合要求的填空 $\text{[math]}$ ； $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

14. 在▱ABCD 中，∠C=45°，AD=BD，P为线段CD上的动点(点P不与点D 重合)，连结 AP，过点P作EP⊥AP交直线BD 于点E.
1. （1）如图1，当P为线段CD的中点时，探究 PA，PE的数量关系，并说明理由.
2. （2）如图2，当点P 在线段CD的任意位置时，求证： $\text{[math]}$
答案解析收藏纠错 + 选题
15. 如图，在平面直角坐标系中，四边形ABCD是平行四边形，A(-3，0)，B(3，0) ，C(0，4)，连结OD，点E是线段0D的中点．
1. （1）求点E和点D的坐标．
2. （2）平面内是否存在一点N，使以C，D，E，N为顶点的四边形是平行四边形？若存在，请求出点N的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题

四、综合题

16. (2023八下·市南区期末) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与x轴、y轴相交于A、B两点，动点C在线段 $\text{[math]}$ 上，将线段 $\text{[math]}$ 绕着点C顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，此时点D恰好落在直线 $\text{[math]}$ 上时，过点D作 $\text{[math]}$ 轴于点E ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求点D的坐标；
3. （3）若点P在y轴上，点Q在直线 $\text{[math]}$ 上，是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q点坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
17. (2023八下·宽城期末) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，动点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，将线段 $\text{[math]}$ 绕着点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，此时点 $\text{[math]}$ 恰好落在直线 $\text{[math]}$ 上，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴于点 $\text{[math]}$ ．
1. （1）求直线 $\text{[math]}$ 的表达式
2. （2）试确定点 $\text{[math]}$ 的坐标；
3. （3）若点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，是否存在以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的 $\text{[math]}$ 点坐标，若不存在，请说明理由．
答案解析收藏纠错 + 选题