河北省邯郸市2024届高三第三次调研考试考试数学试题

更新时间：2024-05-11 浏览次数：37 类型：高考模拟

一、选择题：本题共8小题，每小题5分，共40分在每小题给出的四个选项中，只有一项是符合目要求的．

1. (2024·邯郸三模) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·邯郸三模) 若复数 $\text{[math]}$ 为纯虚数，则实数 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
3. (2024·邯郸三模) 已知向量 $\text{[math]}$ 与 $\text{[math]}$ 共线，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·邯郸三模) 在 $\text{[math]}$ 的展开式中， $\text{[math]}$ 的系数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 6 D . 192

答案解析收藏纠错 + 选题
5. (2024高二下·越秀期中) 已知等比数列 $\text{[math]}$ 的各项互不相等，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等差数列，则 $\text{[math]}$ （）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
6. (2024·邯郸三模) 已知抛物线 $\text{[math]}$ 的焦点为F ， $\text{[math]}$ 为抛物线上一动点，点 $\text{[math]}$ ，则 $\text{[math]}$ 周长的最小值为（）

A . 13 B . 14 C . 15 D . 16

答案解析收藏纠错 + 选题
7. (2024·邯郸三模) 已知 $\text{[math]}$ 是定义在 $\text{[math]}$ 上的偶函数， $\text{[math]}$ ，且 $\text{[math]}$ 在 $\text{[math]}$ 上单调递减，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
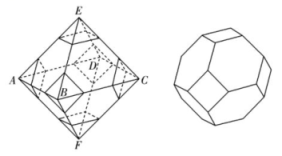
8. (2024·邯郸三模) 已知在四面体 $\text{[math]}$ 中， $\text{[math]}$ ，二面角 $\text{[math]}$ 的大小为 $\text{[math]}$ ，且点A ， B ， C ， D都在球 $\text{[math]}$ 的球面上， $\text{[math]}$ 为棱 $\text{[math]}$ 上一点， $\text{[math]}$ 为棱 $\text{[math]}$ 的中点．若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. (2024高二下·龙门月考) 已知双曲线 $\text{[math]}$ ，则（）

A . $\text{[math]}$ 的取值范围是 $\text{[math]}$ B . $\text{[math]}$ 的焦点可在 $\text{[math]}$ 轴上也可在 $\text{[math]}$ 轴上 C . $\text{[math]}$ 的焦距为6 D . $\text{[math]}$ 的离心率 $\text{[math]}$ 的取值范围为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·邯郸三模) “阿基米德多面体”又称“半正多面体”，与正多面体类似，它们也都是凸多面体，每个面都是正多边形，并且所有棱长也都相等，但不同之处在于阿基米德多面体的每个面的形状不全相同．有几种阿基米德多面体可由正多面体进行“截角”得到如图，正八面体 $\text{[math]}$ 的棱长为3，取各条棱的三等分点，截去六个角后得到一种阿基米德多面体，则该阿基米德多面体（）

A . 共有18个顶点 B . 共有36条棱 C . 表面积为 $\text{[math]}$ D . 体积为 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024·邯郸三模) 已知 $\text{[math]}$ 的三个内角A ， B ， C的对边分别是a ， b ， c ，面积为 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ 的取值范围是 $\text{[math]}$ B . 若 $\text{[math]}$ 为边 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，则 $\text{[math]}$ 的面积的最大值为 $\text{[math]}$ C . 若 $\text{[math]}$ 是锐角三角形，则 $\text{[math]}$ 的取值范围是 $\text{[math]}$ D . 若角 $\text{[math]}$ 的平分线 $\text{[math]}$ 与边 $\text{[math]}$ 相交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为10

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分．

12. (2024·邯郸三模) 写出一个 $\text{[math]}$ ，使得函数 $\text{[math]}$ 的图象关于点 $\text{[math]}$ 对称，则 $\text{[math]}$ 可以为．

答案解析收藏纠错 + 选题
13. (2024·邯郸三模) 从分别写有数字1，2，3，5，9的5张卡片中任取2张，设这2张卡片上的数字之和为 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024·邯郸三模) 记 $\text{[math]}$ 表示x ， y ， z中最小的数．设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．

15. (2024·邯郸三模) 设数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ 是公差为 $\text{[math]}$ 的等差数列．
1. （1）求 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
16. (2024·邯郸三模) 某民营学校为增强实力与影响力，大力招揽名师、建设校园硬件设施，近5年该校招生人数的数据如下表：
年份序号x
1
2
3
4
5
招生人数y/千人
0.8
1
1.3
1.7
2.2
1. （1）由表中数据可看出，可用线性回归模型拟合 $\text{[math]}$ 与 $\text{[math]}$ 的关系，请用相关系数加以证明；
2. （2）求 $\text{[math]}$ 关于 $\text{[math]}$ 的回归直线方程，并预测当年份序号为7时该校的招生人数．
  参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
  参考公式：相关系数 $\text{[math]}$ ，回归方程 $\text{[math]}$ 中斜率和截距的最小二乘估计公式分别为 $\text{[math]}$ ， $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2024·邯郸三模) 如图，在四棱锥 $\text{[math]}$ 中，平面 $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为棱 $\text{[math]}$ 的中点，且 $\text{[math]}$ ．
1. （1）求四棱锥 $\text{[math]}$ 的高；
2. （2）求二面角 $\text{[math]}$ 的正弦值．
答案解析收藏纠错 + 选题
18. (2024·邯郸三模) 已知椭圆 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ 两点．
1. （1）求 $\text{[math]}$ 的方程；
2. （2）若圆 $\text{[math]}$ 的两条相互垂直的切线 $\text{[math]}$ 均不与坐标轴垂直，且直线 $\text{[math]}$ 分别与 $\text{[math]}$ 相交于点A ， C和B ， D ，求四边形 $\text{[math]}$ 面积的最小值．
答案解析收藏纠错 + 选题
19. (2024·邯郸三模) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线方程．
2. （2）已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ 恰有4个不同的实数根 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ．
  （i）求 $\text{[math]}$ 的取值范围；
  （ii）求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题