

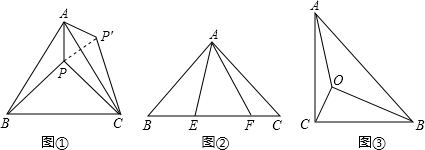
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=;
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
①时,求证:
为等边三角形;
②当 时,
. (直接回答即可)
①点C的坐标为 ▲ , 并求出线段CD所在直线的解析式;
②连接AC、BC,若直线AC的解析式为 , 直线BC的解析式为
, 直接写出关于x的不等式组
的解集.
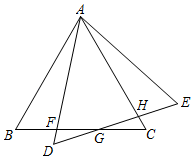
如图,点是
内的一点,将
绕点
逆时针旋转60°到
, 则可以构造出等边
, 得
,
, 所以
的值转化为
的值,当
,
,
,
四点共线时,线段
的长为所求的最小值,即点
为
的“费马点”.
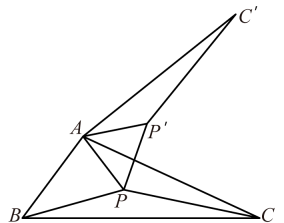
如图1,点是等边
内的一点,连接
,
,
, 将
绕点
逆时针旋转60°得到
.
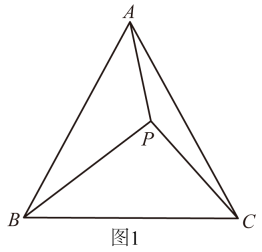
①若 , 则点
与点
之间的距离是 ▲ ;
②当 ,
,
时,求
的大小;