一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
A . 向东走 B . 向南走
B . 向南走 C . 向西走
C . 向西走 D . 向北走
D . 向北走
-
-
3.
(2024·珠海模拟)
近十年来,中国高铁的建设和发展取得了显著的成就,截至2023年1月,中国高铁总里程达到42000公里,稳居世界第一.42000用科学记数法表示为( )
-
-
-
6.
(2024·封开模拟)
在古代,一个国家所算的圆周率

的精确程度,可以作为衡量这个国家当时数学与科技发展的水平的主要标志,我国南北朝时期的祖冲之是世界上最早把圆周率的精确值计算到小数点后第七位的科学巨匠,该成果领先世界一千多年,以下对圆周率的四个表述:①圆周率是一个有理数;②圆周率是一个无理数;③圆周率是一个与圆的大小无关的常数,它等于该圆的周长与直径的比;④圆周率是一个与圆大小有关的常数,它等于该圆的周长与半径的比;其中正确的是( )
A . ①③
B . ②③
C . ①④
D . ②④
-
7.
(2024九下·珠海模拟)
某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为( )
-
-
-
10.
(2024·封开模拟)
如图,在正方形

中,点
B ,
C的坐标分别是

,

, 点
D在抛物线

的图像上,则
b的值是( )

二、填空题:本大题共5小题,每小题3分,共15分.
-
-
-
-
-
15.
(2024·珠海模拟)
如图,在矩形

中,

,

, 对角线

,

相交于点
O , 且

,

. 连接

与

相交于
F . 则图中四边形

的面积为
.

三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.
-
-
(1)
计算:

.
-
(2)
解二元一次方程组

-
17.
(2024·封开模拟)
新农村建设中,在相距

甲、乙两地新修一条高速公路,开通后使甲、乙两地间行驶的长途客运车平均车速提高了

, 从而使得甲地到乙地的时间缩短了

, 求长途客运车原来的平均速度.
-
18.
(2024·封开模拟)
传统工艺品油纸伞是我国的非物质文化遗产,使用历史已有1000多年.伞是由伞柄,伞骨,伞面三部分组成.伞柄是伞的主心骨,伞骨是用来支撑整个伞面的,伞面是伞中重要的组成部分.如图,伞打开时,其伞面的直径

的长为

, 相对两根伞骨的最大夹角

, 求此伞的伞骨

的长度.(结果精确到

, 参考数据:

,

,

).

四、解答题(二):本大题共3小题,每小题9分,共27分.
-
-
(1)
实践与操作:用尺规作图法作线段

的垂直平分线,交

于点
D , 交

于点
E(保留作图痕迹,不要求写作法);
-
(2)
应用与计算:在(1)的条件下,连接

, 若

, 求

的长.
-
-
(1)
探究发现:如图1,在的网格图中,在线段

上求一点
P , 使得

;小明同学发现,先在点
B的左侧取点
C , 使

为1个单位长度,在点
A的右侧取点
D , 使

为2个单位长度,然后连接

交

于点
P(如图1),就可以得到点
P了,请你验证小明的做法,并求出

的值.
-
(2)
请你在图2中线段

上求作一点
P , 使得

.
-
21.
(2024·封开模拟)
学校为了选拔一位初中学生参加县运动会实心球项目比赛,记录了两位优秀同学五次投掷数据(单位:米)
运动员 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
华兴 | 13 | 12 | 13 | 11 | 15 |
强华 | 14 | 13 | 12 | 13 | 13 |
-
(1)
华兴同学投掷实心球数据的众数;强华同学投掷实心球数据的中位数.
-
(2)
如果你是教练会选择哪位同学参加此次县运动会该项目比赛?说说你的理由(往年该项目比赛最好成绩是13.2米).
五、解答题(三):本大题共2小题,每小题12分,共24分.
-
-
-
(2)
求证:

为

的切线;
-
(3)
求证:点
F为线段

的中点.
-
-
(1)
如图1,求证:

;
-
-
(3)
如图3,连接

, 在折叠的过程中,满足下面条件情况下直接写出

长.
①当 为以
为以 为顶点的等腰三角形时,
为顶点的等腰三角形时, 长是多少?
长是多少?
②当 为以B为顶点的等腰三角形时,
为以B为顶点的等腰三角形时, 长是多少?
长是多少?
 B .
B . 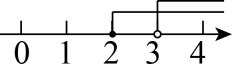 C .
C . 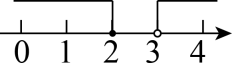 D .
D . 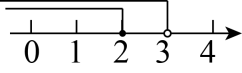


为以
为顶点的等腰三角形时,
长是多少?
为以B为顶点的等腰三角形时,
长是多少?