湖北省随州市曾都区2023-2024学年八年级上学期期末数学...

更新时间：2025-01-02 浏览次数：15 类型：期末考试

一、选择题（本题共10小题，每小题3分，共30分．每小题给出的四个选项中只有一项是符合题目要求的）

1. (2024八上·随州期中) 若一个三角形的两边长分别是3和4，则第三边的长可能是（）

A . 1 B . 2 C . 7 D . 8

答案解析收藏纠错 + 选题
2. (2024八上·曾都期末) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八上·曾都期末) 近年来教育主管部门高度重视校园安全教育，各级各类学校从认识安全警告标志入手开展安全教育，下列安全图标不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024八上·曾都期末) 在下列多项式中，与-x-y相乘的结果为x²－y²的多项式是（）

A . x－y B . x＋y C . –x＋y D . –x－y

答案解析收藏纠错 + 选题
5. (2024八下·济南期中) 化简 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八上·沾益期末) 一个多边形的内角和比它的外角和的 $\text{[math]}$ 倍少 $\text{[math]}$ ，则这个多边形的边数是（）

A . 七 B . 八 C . 九 D . 十

答案解析收藏纠错 + 选题
7. (2024八上·曾都期末) 已知一个三角形三边长分别是4，9，12，要作最长边上的高正确的图形做法是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2024八上·曾都期末) 在“单项式乘多项式”的课堂上，有这样一道题的计算过程： $\text{[math]}$ “□”内应填的符号为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024八上·曾都期末) 如图， $\text{[math]}$ 于P ， $\text{[math]}$ ，添加下列一个条件，能利用“ $\text{[math]}$ ”判定 $\text{[math]}$ 的条件是（）

A . $\text{[math]}$ B . $\text{[math]}$ 与 $\text{[math]}$ 互余 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024八上·曾都期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是高， $\text{[math]}$ 是角平分线， $\text{[math]}$ 是中线， $\text{[math]}$ 与 $\text{[math]}$ 交于点M ， $\text{[math]}$ 与 $\text{[math]}$ 交于点N ，连接 $\text{[math]}$ ．下列说法正确的有（）
① $\text{[math]}$ ；
② $\text{[math]}$ ；
③ $\text{[math]}$ ；④若 $\text{[math]}$ ，则 $\text{[math]}$ ．

A . ①②③④ B . ①②③ C . ①②④ D . ①③④

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共18分．把正确答案填在答题卡对应题号的横线上）

11. (2024八上·曾都期末) 石墨烯是现在世界上最薄的纳米材料，其理论厚度仅有 $\text{[math]}$ 米，将数据 $\text{[math]}$ 米用科学记数法表示为米．

答案解析收藏纠错 + 选题
12. (2024八上·曾都期末) 若m ， n为常数，多项式 $\text{[math]}$ 可因式分解为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2024八上·曾都期末) 式子 $\text{[math]}$ 有意义的条件是．

答案解析收藏纠错 + 选题
14. (2024八上·曾都期末) “三等分角”是古希腊三大几何问题之一．如图这个“三等分角仪”由两根有槽的棒 $\text{[math]}$ 组成，两根棒在O点相连并可绕O转动，C点固定， $\text{[math]}$ ，点D ， E可在槽中滑动，若 $\text{[math]}$ ，则 $\text{[math]}$ °．

答案解析收藏纠错 + 选题
15. (2024八上·曾都期末) 用一条长为 $\text{[math]}$ $\text{[math]}$ 的细绳围成一个等腰三角形，已知这个等腰三角形一边长是另一边长的 $\text{[math]}$ 倍，则它的腰长为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024八上·曾都期末) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点M ， N分别在 $\text{[math]}$ ， $\text{[math]}$ 上，当 $\text{[math]}$ 的周长最小时， $\text{[math]}$ 的度数为度．

答案解析收藏纠错 + 选题

三、解答题（本题共8小题，共72分．解答应写出必要的演算步骤、文字说明或证明过程）

17. (2024八上·曾都期末) 按要求解下列各题：
1. （1）计算： $\text{[math]}$ ；
2. （2）因式分解： $\text{[math]}$ ；
3. （3）先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024八上·曾都期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ．
1. （1）过点B作 $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点D（尺规作图，保留作图痕迹，标注有关字母，不用写作法和证明）；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
19. (2024八上·曾都期末) 生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察生活，就会有许多意想不到的收获．下面用一副三角板（ $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ； $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ）拼接图形．
1. （1）如图 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，求 $\text{[math]}$ 的度数；
2. （2）如图 $\text{[math]}$ ，点 $\text{[math]}$ 与点 $\text{[math]}$ 重合， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，判断并证明 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系．
答案解析收藏纠错 + 选题
20. (2024八上·曾都期末) 已知在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）如图 $\text{[math]}$ ，求证： $\text{[math]}$ 为等腰三角形；
2. （2）如图 $\text{[math]}$ ，当 $\text{[math]}$ 时，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，在不添加任何辅助线的情况下，请直接写出图 $\text{[math]}$ 中所有顶角等于 $\text{[math]}$ 的等腰三角形．
答案解析收藏纠错 + 选题
21. (2024八上·曾都期末) 观察以下等式：
第 $\text{[math]}$ 个等式： $\text{[math]}$ ，第 $\text{[math]}$ 个等式： $\text{[math]}$ ，第 $\text{[math]}$ 个等式： $\text{[math]}$ ，
第 $\text{[math]}$ 个等式： $\text{[math]}$ ，第 $\text{[math]}$ 个等式： $\text{[math]}$
1. （1）按照以上规律，接着再写两个等式；
2. （2）写出你猜想到的第 $\text{[math]}$ 个等式（用含 $\text{[math]}$ 的等式表示）；
3. （3）运用有关知识，推理证明（2）中的猜想是正确的．
答案解析收藏纠错 + 选题
22. (2024八上·曾都期末) 甲、乙两人加工同一种零件，乙每天加工的数量比甲每天加工数量多 $\text{[math]}$ ，两人各加工 $\text{[math]}$ 个这种零件，甲比乙多用5天．
1. （1）求甲、乙两人每天各加工多少个这种零件？
2. （2）现有 $\text{[math]}$ 个这种零件的加工任务，由甲单独加工m天后剩余任务由乙单独完成，试用含m的代数式表示乙单独完成剩余任务的天数（结果要求化简）；
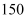
3. （3）已知甲、乙两人加工这种零件每天的加工费分别是 $\text{[math]}$ 元和 $\text{[math]}$ 元，在（2）的情况下，如果总加工费不超过 $\text{[math]}$ 元，那么甲最多加工多少天？
答案解析收藏纠错 + 选题
23. (2024七下·榕城期中) 有两类正方形A ， B ，其边长分别为a ， b（ $\text{[math]}$ ），现将B放在A的内部得图甲，将A ， B并列放置后构造新的正方形得图乙，若图甲和图乙中阴影部分的面积分别为4和16．
1. （1）用含a ， b的代数式分别表示甲图中阴影部分的面积为，乙图中阴影部分的面积为；
2. （2）求正方形A ， B的面积之和；
3. （3）三个正方形A和两个正方形B如图丙摆放，求阴影部分的面积．
答案解析收藏纠错 + 选题
24. (2024八上·曾都期末) 在锐角 $\text{[math]}$ 中，分别以 $\text{[math]}$ ， $\text{[math]}$ 为边向外作等边 $\text{[math]}$ 和等边 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ．
1. （1）如图1，易证 $\text{[math]}$ ，其依据是，从而得出结论： $\text{[math]}$ $\text{[math]}$ 与 $\text{[math]}$ $\text{[math]}$ （用“ $\text{[math]}$ ”、“ $\text{[math]}$ ”或“ $\text{[math]}$ ”填空）；
2. （2）如图2，若 $\text{[math]}$ ，请探究线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系及直线 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并给出证明；
3. （3）在（2）的条件下，若 $\text{[math]}$ 交于 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ （如图2），试探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间存在的等量关系，并给予证明．
答案解析收藏纠错 + 选题