 B .
B . 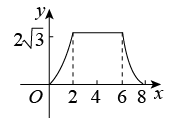 C .
C . 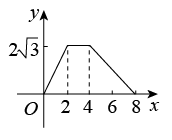 D .
D . 

 B .
B .  C .
C .  D .
D . 
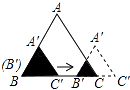
 B .
B . 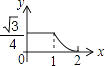 C .
C . 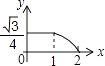 D .
D . 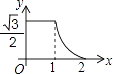
 B .
B .  C .
C .  D .
D . 
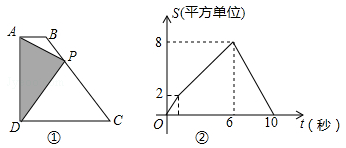
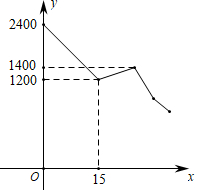
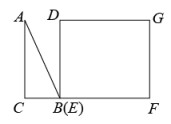
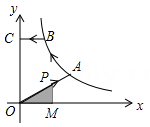
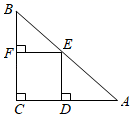
规定:t秒时,甲到达的位置记为点A,乙到达的位置记为点B,例如,1秒时,甲到达的位置记为A,乙到达的位置记为B,(如图所示);2.5秒时,甲到达的位置记为A2.5等等.容易知道,两条平行且相等的线段,其中包含有相同的方位信息所以,在研究有关运动问题时,为研究方便,我们可把点或线段进行合适的平移后,再去研究(物理上的相对运动观,就是源于这种数学方法)现对t秒时,甲、乙到达的位置点At , Bt , 按如下步骤操作:
第一步:连接AtBt;
第二步:把线段AtBt进行平移,使点Bt与点B重合,平移后,点A1的对应点用点At’标记
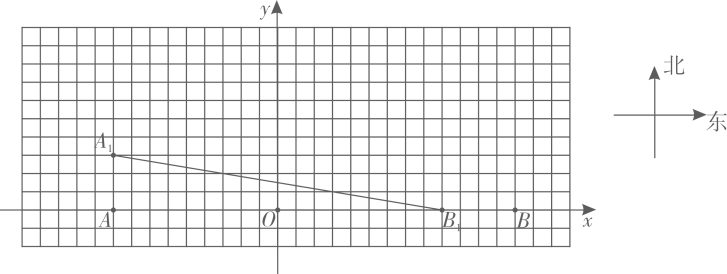
解答下列问题:
①利用网格,在上图中画出A1 , B1经过上述第二步操作后的图形;
②此时,甲在乙的什么方位?(请填空)
答:此时,甲在乙的北偏西θ°(其中tanθ°= , 两者相距 个单位长度.
|
t的取值 |
1 |
2 |
3 |
t |
|
点At'的坐标 |
(-5,3) |
( , ) |
( , ) |
( , ) |
①如果把点At'的横、纵坐标分别用变量x,y表示,则y与x之间的函数关系式为;
②点A3.5’的坐标为
请解答:运动过程中,甲、乙之间的最近距离为个单位长度.
解:∵ , ∴
.
∵ , ∴
.
若函数 , 求y的取值范围.

①列表:下表列出点与R的几组对应值,请写出m,n的值:
,
;
|
R |
… |
3 |
4 |
5 |
6 |
… |
|
|
… |
2 |
1.5 |
1.2 |
1 |
… |
|
|
… |
3 |
m |
2.2 |
n |
… |
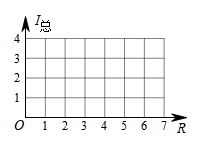
②描点、连线:在平面直角坐标系中,以①给出的R的取值为横坐标,以相对应的值为纵坐标,描出相应的点,并将各点用光滑曲线顺次连接起来 ;
①随R的增大而;(填“增大”或“减小”)
②函数的图象是由
的图象向平移个单位而得到.
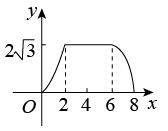
实验观察:实验小组通过观察,每两小时记录一次电子秤读数,得到下表.
|
漏沙时间x(h) |
0 |
2 |
4 |
6 |
8 |
|
电子秤读数y(克) |
6 |
18 |
30 |
42 |
54 |


①列表:下表列出 点与R的几组对应值,请写出m,n的值:
,
;
| R | … | 3 | 4 | 5 | 6 | … |
| | … | 2 | 1.5 | 1.2 | 1 | … |
| | … | 3 | m | 2.2 | n | … |

②描点、连线:在平面直角坐标系中,以①给出的R的取值为横坐标,以 相对应的值为纵坐标,描出相应的点,并将各点用光滑曲线顺次连接起来;
① 随R的增大而;(填“增大”或“减小”)
②函数 的图象是由
的图象向平移个单位而得到.
列表:下表是x与y的几组对应值,其中m=.
|
x |
… |
﹣3 |
﹣2 |
﹣1 |
|
|
1 |
2 |
3 |
… |
|
y |
… |
|
1 |
2 |
4 |
4 |
2 |
1 |
m |
… |
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出各点,请你描出剩下的点;
连线:用平滑的曲线顺次连接各点,已经画出了部分图象,请你把图象补充完整;

①函数值y随x的增大而增大;②关于y轴对称;③
关于原点对称;