广东省汕头市潮阳第一中学2023-2024学年高二下学期4月...

更新时间：2024-06-18 浏览次数：8 类型：期中考试

一、单选题：本题共8小题，每小题5分，共40分，在每小题给出的选项中，只有一项符合题目要求.

1. (2024高二下·潮阳期中) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ， C=A∩B，则集合C的真子集个数为（）

A . 2 B . 3 C . 4 D . 8

答案解析收藏纠错 + 选题
2. (2024高二下·潮阳期中) 已知复数 $\text{[math]}$ 满足 $\text{[math]}$ （ $\text{[math]}$ 为虚数单位），则 $\text{[math]}$ 的虚部为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高二下·潮阳期中) 函数 $\text{[math]}$ 的导函数 $\text{[math]}$ 的图像如图所示，以下命题正确的是（）

A . $\text{[math]}$ 是函数的最小值 B . $\text{[math]}$ 是函数的极值 C . $\text{[math]}$ 在区间 $\text{[math]}$ 上不单调 D . $\text{[math]}$ 在 $\text{[math]}$ 处的切线的斜率大于0

答案解析收藏纠错 + 选题
4. (2024高一下·东莞期中) 已知按从小到大顺序排列的两组数据：
甲组：27，30，37，a ， 40，50；乙组：24，b ， 33，44，48，52．
若这两组数据的第30百分位数对应相等，第50百分位数也对应相等，则a+b=（）

A . 60 B . 65 C . 70 D . 75

答案解析收藏纠错 + 选题
5. (2024高二下·潮阳期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高二下·潮阳期中) 某国军队计划将5艘不同的军舰全部投入到甲，乙，丙三个海上区域进行军事演习，要求每个区域至少投入一艘军舰，且军舰A必须安排在甲区域，则甲区域还有其它军舰的安排方案共有（）

A . 50种 B . 36种 C . 24种 D . 14种

答案解析收藏纠错 + 选题
7. (2024高二下·潮阳期中) 已知椭圆 $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ， P为椭圆上一点，且 $\text{[math]}$ ，若 $\text{[math]}$ 关于 $\text{[math]}$ 平分线的对称点在椭圆C上，则该椭圆的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二下·潮阳期中) 设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对得6分，部分选对得部分分，有选错得0分.

9. (2024高二下·潮阳期中) 已知 $\text{[math]}$ 的展开式中，各项的二项式系数之和为64，则（）

A . $\text{[math]}$ B . 只有第4项的二项式系数最大 C . 若展开式中各项系数之和为64，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则展开式中常数项为15

答案解析收藏纠错 + 选题
10. (2024高二下·潮阳期中) 已知正方体 $\text{[math]}$ 的棱长为3，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上靠近 $\text{[math]}$ 点的三等分点， $\text{[math]}$ 是 $\text{[math]}$ 中点，则（）

A . 直线 $\text{[math]}$ 与 $\text{[math]}$ 所成角的正切值为 $\text{[math]}$ B . 三棱柱 $\text{[math]}$ 外接球的半径为 $\text{[math]}$ C . 平面 $\text{[math]}$ 截正方体所得截面为等腰梯形 D . 点 $\text{[math]}$ 到平面 $\text{[math]}$ 的距离为 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高二下·潮阳期中) 已知函数 $\text{[math]}$ ，其中 $\text{[math]}$ ，则（）．

A . 不等式 $\text{[math]}$ 对 $\text{[math]}$ 恒成立 B . 若直线 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象有且只有两个不同的公共点，则k的取值范围是 $\text{[math]}$ C . 方程 $\text{[math]}$ 恰有3个实根 D . 若关于x的不等式 $\text{[math]}$ 恰有1个负整数解，则a的取值范围为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分.

12. (2024高二下·潮阳期中) 若直线 $\text{[math]}$ 是曲线 $\text{[math]}$ 的一条切线，则实数 $\text{[math]}$ 的值为

答案解析收藏纠错 + 选题
13. (2024高二下·潮阳期中) 《莱茵德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题目：把100个面包分给5个人，使每人所得份量成等差数列，且较大的三份之和的 $\text{[math]}$ 是较小的两份之和，则最小一份的量为.

答案解析收藏纠错 + 选题
14. (2024高二下·潮阳期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ，点Q满足 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为.

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分.解答时应写出说明、证明过程或必要的演算步骤.

15. (2024高二下·潮阳期中) 在△ABC中，角A ， B ， C的对边长依次是a ， b ， c ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求角B的大小；
2. （2）若AD是∠BAC的内角平分线，当△ABC面积最大时，求AD的长．
答案解析收藏纠错 + 选题
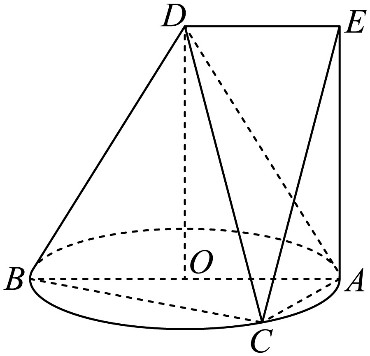
16. (2024高二下·潮阳期中) 如图，在圆锥DO中，D为圆锥顶点，AB为圆锥底面的直径，O为底面圆的圆心，C为底面圆周上一点，四边形OAED为矩形．
1. （1）求证：平面BCD⊥平面ACE；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求平面ADE和平面CDE夹角的余弦值
答案解析收藏纠错 + 选题
17. (2024高二下·潮阳期中) 已知数列 $\text{[math]}$ 的首项 $\text{[math]}$ ，且满足 $\text{[math]}$ .
1. （1）判断数列 $\text{[math]}$ 是否为等比数列；
2. （2）若 $\text{[math]}$ ，记数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2024高二下·潮阳期中) 已知双曲线C： $\text{[math]}$ 上任意一点Q（异于顶点）与双曲线两顶点连线的斜率之积为 $\text{[math]}$ . E在双曲线C上，F为双曲线C的右焦点，|EF|的最小值为 $\text{[math]}$ .
1. （1）求双曲线C的标准方程；
2. （2）过椭圆 $\text{[math]}$ 上任意一点P（P不在C的渐近线上）分别作平行于双曲线两条渐近线的直线，交两渐近线于M ， N两点，且 $\text{[math]}$ ，是否存在m ， n使得椭圆的离心率为 $\text{[math]}$ ？若存在，求出椭圆的方程，若不存在，说明理由.
答案解析收藏纠错 + 选题
19. (2024高二下·东坡期末) 已知函数 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的极值；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 在 $\text{[math]}$ 上的最小值；
3. （3）若 $\text{[math]}$ 在 $\text{[math]}$ 上存在零点，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题