题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

四川省自贡市蜀光绿盛实验学校2023-2024学年七年级下学...

更新时间：2024-05-28 浏览次数：19 类型：月考试卷

一、选择题（本题有8个小题，每小题3分，满分24分，每个小题只有一个选项符合题意）

1. (2024七下·环江期中) 4的算术平方根是（）

A . 2　　 B . ±2　　 C . $\text{[math]}$ 　　 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七下·自贡月考) 下列大学校徽可以看成是由图案自身的一部分经平移后得到的为（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024七下·自贡月考) 如图，直线 $\text{[math]}$ ，直线 $\text{[math]}$ 、 $\text{[math]}$ 被直线 $\text{[math]}$ 所截，若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·自贡月考) 如图，下列条件能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·凉州期中) 在 $\text{[math]}$ ， $\text{[math]}$ ， 1.732， $\text{[math]}$ ， $\text{[math]}$ ， 3.1010010001……， $\text{[math]}$ 中无理数有（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
6. (2024七下·自贡月考) 下列命题是真命题的是（　　）

A . 钝角没有余角 B . 同旁内角相等，两直线平行 C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 过一点有且只有一条直线与已知直线平行

答案解析收藏纠错 + 选题
7. (2024七下·吴兴期中) 如图，两个完全一样的直角三角形重叠在一起，将其中的一个三角形沿着点 $\text{[math]}$ 到点 $\text{[math]}$ 的方向平移到 $\text{[math]}$ 的位置， $\text{[math]}$ ， $\text{[math]}$ ，平移距离为6，则阴影部分面积为（）

A . 60 B . 96 C . 84 D . 42

答案解析收藏纠错 + 选题
8. (2024七下·自贡月考) 如图1是长方形纸带，∠DEF＝10°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是多少（）

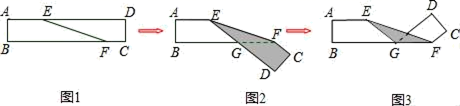
A . 160° B . 150° C . 120° D . 110°

答案解析收藏纠错 + 选题

二、填空题（本题有6个小题，每小题3分，共计18分）

9. (2024七下·崇义期中) 将命题“对顶角相等”改写为“如果……那么……”的形式，可写为．

答案解析收藏纠错 + 选题
10. (2024七下·自贡月考) 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是．

答案解析收藏纠错 + 选题
11. (2024七下·自贡月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024·瑞昌模拟) 如图，平行于主光轴 $\text{[math]}$ 的光线 $\text{[math]}$ 和 $\text{[math]}$ 经过凹透镜的折射后，折射光线 $\text{[math]}$ 的反向延长线交于主光轴 $\text{[math]}$ 上一点P ． $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是．

答案解析收藏纠错 + 选题
13. (2024七下·自贡月考) 对于任意两个不相等的实数 $\text{[math]}$ 、 $\text{[math]}$ ，定义一种新运算“ $\text{[math]}$ ”如下： $\text{[math]}$ ，如： $\text{[math]}$ ．那么 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024七下·自贡月考) 一副三角板按如图所示叠放在一起，其中点 $\text{[math]}$ ， $\text{[math]}$ 重合，若固定三角板 $\text{[math]}$ ，将三角板 $\text{[math]}$ 绕着公共顶点 $\text{[math]}$ ，按逆时针方向旋转 $\text{[math]}$ 度（ $\text{[math]}$ ），当旋转后的 $\text{[math]}$ 与三角板 $\text{[math]}$ 的某一边平行时， $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题（本题有5个小题，每小题5分，共计25分）

15. (2024七下·自贡月考) 计算 $\text{[math]}$ - $\text{[math]}$ =.

答案解析收藏纠错 + 选题
16. (2024七下·自贡月考) 已知 $\text{[math]}$ 的立方根是 $\text{[math]}$ ， $\text{[math]}$ 是16的算术平方根，求 $\text{[math]}$ 的平方根．

答案解析收藏纠错 + 选题
17. (2024七下·自贡月考) 已知一个正数m的两个平方根是 $\text{[math]}$ 和 $\text{[math]}$ ，求m的值．

答案解析收藏纠错 + 选题
18. (2024七下·德庆期中) 如图， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
19. (2024七下·自贡月考) 如图，若 $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 吗？请在下面的解答过程中填空或在括号内填写理由．
解：理由如下：
$\text{[math]}$ （已知），
$\text{[math]}$ $\text{[math]}$ （），
$\text{[math]}$ $\text{[math]}$ （）
又 $\text{[math]}$ （已知），
$\text{[math]}$ $\text{[math]}$ （）
$\text{[math]}$ （）．

答案解析收藏纠错 + 选题

四、解答题（本题有3个小题，每小题6分，共计18分）

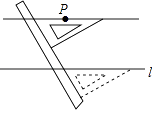
20. (2024七下·自贡月考) 如图，点P，点Q分别代表两个村庄，直线l代表两个村庄中间的一条公路．根据居民出行的需要，计划在公路l上的某处设置一个公交站．
1. （1）若考虑到村庄P居住的老年人较多，计划建一个离村庄P最近的车站，请在公路l上画出车站的位置（用点M表示），依据是 ▲ ；
2. （2）若考虑到修路的费用问题，希望车站的位置到村庄P和村庄Q的距离之和最小，请在公路l上画出车站的位置（用点N表示），依据是 ▲ ．
答案解析收藏纠错 + 选题
21. (2024七下·宁乡市期中) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，垂足为 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求∠COB的度数
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
22. (2024七下·自贡月考) 已知如图，已知 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）判断 $\text{[math]}$ 与 $\text{[math]}$ 是否平行，并说明理由；
2. （2）求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题

五、解答下列各题（本题共有2个小题，第23题7分，第24题8分，共计15分）

23. (2024七下·自贡月考) 阅读下面的文字，解答问题：
大家知道 $\text{[math]}$ 是无理数，而无理数是无限不循环小数，因此V2的小数部分我们不可能全部地写出来，于是小明用 $\text{[math]}$ 来表示 $\text{[math]}$ 的小数部分，你同意小明的表示方法吗?
事实上，小明的表示方法是有道理，因为 $\text{[math]}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．
又例如：∵ $\text{[math]}$ ，即 $\text{[math]}$ ，
∴ $\text{[math]}$ 的整数部分为2，小数部分为 $\text{[math]}$ ．
请解答：
1. （1）如果 $\text{[math]}$ 的小数部分为 $\text{[math]}$ ， $\text{[math]}$ 的整数部分为 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）已知： $\text{[math]}$ ，其中 $\text{[math]}$ 是整数，且 $\text{[math]}$ ，求 $\text{[math]}$ 的相反数．
答案解析收藏纠错 + 选题
24. (2024七下·自贡月考) 已知：直线 $\text{[math]}$ ，点E ， F分别在直线AB ， CD上，点M为两平行线内部一点．
1. （1）如图1，∠AEM ， ∠M ， ∠CFM的数量关系为；(直接写出答案)
2. （2）如图2，∠MEB和∠MFD的角平分线交于点N ，若∠EMF等于130°，求∠ENF的度数；
3. （3）如图3，点G为直线CD上一点，延长GM交直线AB于点Q ，点P为MG上一点，射线PF、EH相交于点H ，满足 $\text{[math]}$ ， $\text{[math]}$ ，设∠EMF=α，求∠H的度数(用含α的代数式表示)．
答案解析收藏纠错 + 选题

试卷信息