2014年高考理数真题试卷（重庆卷）

更新时间：2016-10-19 浏览次数：878 类型：高考真卷

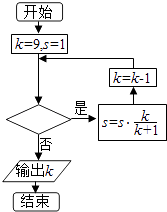
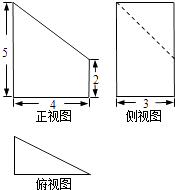
一、选择题：在每小题给出的四个备选项中，只有一项是符合题目要求的．

1. (2014·重庆理) 在复平面内复数Z=i（1﹣2i）对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
2. (2014·重庆理) 对任意等比数列{a_n}，下列说法一定正确的是（）

A . a₁ ， a₃ ， a₉成等比数列 B . a₂ ， a₃ ， a₆成等比数列 C . a₂ ， a₄ ， a₈成等比数列 D . a₃ ， a₆ ， a₉成等比数列

答案解析收藏纠错 + 选题
3. (2014·重庆理) 已知变量x与y正相关，且由观测数据算得样本平均数 $\text{[math]}$ =3， $\text{[math]}$ =3.5，则由该观测数据算得的线性回归方程可能是（）

A . $\text{[math]}$ =0.4x+2.3 B . $\text{[math]}$ =2x﹣2.4 C . $\text{[math]}$ =﹣2x+9.5 D . $\text{[math]}$ =﹣0.3x+4.4

答案解析收藏纠错 + 选题
4. (2014·重庆理) 已知向量 $\text{[math]}$ =（k，3）， $\text{[math]}$ =（1，4）， $\text{[math]}$ =（2，1）且（2 $\text{[math]}$ ﹣3 $\text{[math]}$ ）⊥ $\text{[math]}$ ，则实数k=（）

A . ﹣ $\text{[math]}$ B . 0 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2014·重庆理) 执行如图所示的程序框图，若输出k的值为6，则判断框内可填入的条件是（）

A . s＞ $\text{[math]}$ B . s＞ $\text{[math]}$ C . s＞ $\text{[math]}$ D . s＞ $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2014·重庆理) 已知命题p：对任意x∈R，总有2^x＞0，q：“x＞0”是“x＞2”的充分不必要条件，则下列命题为真命题的是（）

A . p∧q B . （￢p）∧（￢q） C . （￢p）∧q D . p∧（￢q）

答案解析收藏纠错 + 选题
7. (2014·重庆理) 某几何体的三视图如图所示则该几何体的表面积为（）

A . 54 B . 60 C . 66 D . 72

答案解析收藏纠错 + 选题
8. (2014·重庆理) 设F₁ ， F₂分别为双曲线 $\text{[math]}$ （a＞0，b＞0）的左、右焦点，双曲线上存在一点P使得|PF₁|+|PF₂|=3b，|PF₁|•|PF₂|= $\text{[math]}$ ab，则该双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
9. (2014·重庆理) 某次联欢会要安排3个歌舞类节目，2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法种数是（）

A . 72 B . 120 C . 144 D . 168

答案解析收藏纠错 + 选题
10. (2014·重庆理) 已知△ABC的内角A，B，C满足sin2A+sin（A﹣B+C）=sin（C﹣A﹣B）+ $\text{[math]}$ ，面积S满足1≤S≤2，记a，b，c分别为A，B，C所对的边，在下列不等式一定成立的是（）

A . bc（b+c）＞8 B . ab（a+b）＞16 $\text{[math]}$ C . 6≤abc≤12 D . 12≤abc≤24

答案解析收藏纠错 + 选题

二、填空题

11. (2014·重庆理) 设全集U={n∈N|1≤n≤10}，A={1，2，3，5，8}，B={1，3，5，7，9}，则（∁_UA）∩B=．

答案解析收藏纠错 + 选题
12. (2014·重庆理) 函数f（x）=log₂ $\text{[math]}$ • $\text{[math]}$ （2x）的最小值为．

答案解析收藏纠错 + 选题
13. (2014·重庆理) 已知直线ax+y﹣2=0与圆心为C的圆（x﹣1）²+（y﹣a）²=4相交于A，B两点，且△ABC为等边三角形，则实数a=．

答案解析收藏纠错 + 选题

三、选做题：考生注意（14）（15）、（16）三题为选做题，请从中任选两题作答，若三题全做，则按前两题给分

14. (2014·重庆理) 过圆外一点P作圆的切线PA（A为切点），再作割线PBC依次交圆于B、C，若PA=6，AC=8，BC=9，则AB=．

答案解析收藏纠错 + 选题
15. (2014·重庆理) 已知直线l的参数方程为 $\text{[math]}$ （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin²θ﹣4cosθ=0（ρ≥0，0≤θ＜2π），则直线l与曲线C的公共点的极径ρ=．

答案解析收藏纠错 + 选题
16. (2014·重庆理) 若不等式|2x﹣1|+|x+2|≥a²+ $\text{[math]}$ a+2对任意实数x恒成立，则实数a的取值范围是．

答案解析收藏纠错 + 选题

四、解答题：解答应写出文字说明、证明过程或演算步骤．

17. (2014·重庆理) 已知函数f（x）= $\text{[math]}$ sin（ωx+φ）（ω＞0，﹣ $\text{[math]}$ ≤φ＜ $\text{[math]}$ ）的图象关于直线x= $\text{[math]}$ 对称，且图象上相邻两个最高点的距离为π．
1. （1）求ω和φ的值；
2. （2）若f（ $\text{[math]}$ ）= $\text{[math]}$ （ $\text{[math]}$ ＜α＜ $\text{[math]}$ ），求cos（α+ $\text{[math]}$ ）的值．
答案解析收藏纠错 + 选题
18. (2014·重庆理) 一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3，从盒中任取3张卡片．
1. （1）求所取3张卡片上的数字完全相同的概率；
2. （2） X表示所取3张卡片上的数字的中位数，求X的分布列与数学期望．（注：若三个数字a，b，c满足a≤b≤c，则称b为这三个数的中位数．）
答案解析收藏纠错 + 选题
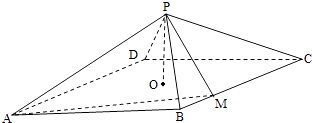
19. (2014·重庆理) 如图，四棱锥P﹣ABCD，底面是以O为中心的菱形，PO⊥底面ABCD，AB=2，∠BAD= $\text{[math]}$ ，M为BC上的一点，且BM= $\text{[math]}$ ，MP⊥AP．
1. （1）求PO的长；
2. （2）求二面角A﹣PM﹣C的正弦值．
答案解析收藏纠错 + 选题
20. (2014·重庆理) 已知函数f（x）=ae^2x﹣be^﹣^2x﹣cx（a，b，c∈R）的导函数f′（x）为偶函数，且曲线y=f（x）在点（0，f（0））处的切线的斜率为4﹣c．
1. （1）确定a，b的值；
2. （2）若c=3，判断f（x）的单调性；
3. （3）若f（x）有极值，求c的取值范围．
答案解析收藏纠错 + 选题
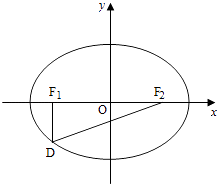
21. (2014·重庆理) 如图，设椭圆 $\text{[math]}$ （a＞b＞0）的左、右焦点分别为F₁ ， F₂ ，点D在椭圆上．DF₁⊥F₁F₂ ， $\text{[math]}$ =2 $\text{[math]}$ ，△DF₁F₂的面积为 $\text{[math]}$ ．
1. （1）求椭圆的标准方程；
2. （2）设圆心在y轴上的圆与椭圆在x轴的上方有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点，求圆的半径．
答案解析收藏纠错 + 选题
22. (2014·重庆理) 设a₁=1，a_n+1= $\text{[math]}$ +b（n∈N^*）
1. （1）若b=1，求a₂ ， a₃及数列{a_n}的通项公式；
2. （2）若b=﹣1，问：是否存在实数c使得a_2n＜c＜a_2n+1对所有的n∈N^*成立，证明你的结论．
答案解析收藏纠错 + 选题