浙江省杭州市浙里特色联盟2023-2024学年高二下学期4月...

更新时间：2024-05-22 浏览次数：22 类型：期中考试

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

1. (2024高二下·杭州期中) 若集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高二下·杭州期中) 在等差数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . 13 B . 14 C . 16 D . 17

答案解析收藏纠错 + 选题
3. (2024高二下·杭州期中) 已知空间向量 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ 与 $\text{[math]}$ 夹角的余弦值为 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高二下·印江月考) 若函数 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高二下·杭州期中) 若点 $\text{[math]}$ 是角 $\text{[math]}$ 终边上一点，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . -2 D . 2

答案解析收藏纠错 + 选题
6. (2024高二下·杭州期中) 已知圆 $\text{[math]}$ 与圆 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，则直线 $\text{[math]}$ 的方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高二下·杭州期中) 我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来研究函数图象的特征．我们从这个商标中抽象出一个图象如图，其对应的函数可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二下·杭州期中) 已知抛物线C： $\text{[math]}$ 的焦点F到准线的距离为4，过点F的直线与抛物线交于A ， B两点，M为线段 $\text{[math]}$ 的中点，若 $\text{[math]}$ ，则点M到y轴的距离为（）

A . 4 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题

二、多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. (2024高二下·杭州期中) 已知复数 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ 的实部为1 B . $\text{[math]}$ 在复平面内对应的点位于第四象限 C . $\text{[math]}$ 的虚部为 $\text{[math]}$ D . $\text{[math]}$ 的共轭复数为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高二上·佛山月考) 袋子中共有大小和质地相同的4个球，其中2个白球和2个黑球，从袋中有放回地依次随机摸出2个球．甲表示事件“第一次摸到白球”，乙表示事件“第二次摸到黑球”，丙表示事件“两次都摸到白球”，则（）

A . 甲与乙互斥 B . 乙与丙互斥 C . 甲与乙独立 D . 甲与乙对立

答案解析收藏纠错 + 选题
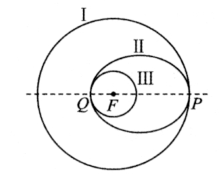
11. (2024高二下·杭州期中) 如图所示，“嫦娥五号”月球探测器飞行到月球附近时，首先在以月球球心F为圆心的圆形轨道I上绕月球飞行，然后在P点处变轨进入以F为一个焦点的椭圆轨道Ⅱ绕月球飞行，最后在Q点处变轨进入以F为圆心的圆形轨道Ⅲ绕月球飞行，设圆形轨道I的半径为R ，圆形轨道Ⅲ的半径为r ，则（）

A . 轨道I的长轴长为 $\text{[math]}$ B . 轨道Ⅱ的焦距为 $\text{[math]}$ C . 若R不变，r越小，轨道Ⅱ的短轴长越大 D . 若r不变，R越大，轨道Ⅱ的离心率越小

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分.

12. (2024高二下·杭州期中) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2024高二下·杭州期中) 已知直线 $\text{[math]}$ ： $\text{[math]}$ .若点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，则数列 $\text{[math]}$ 的前n项和 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2024高二下·杭州期中) 古希腊数学家阿波罗尼斯（约公元前262～公元前190年）的著作《圆锥曲线论》是古代数学的重要成果，其中有这样一个结论：平面内与两点距离的比为常数 $\text{[math]}$ 的点的轨迹是圆，后人岗称这个圆为阿波罗尼斯圆，已知点 $\text{[math]}$ ， $\text{[math]}$ ，动点 $\text{[math]}$ 满足 $\text{[math]}$ ，则点P的轨迹与圆C： $\text{[math]}$ 的公切线的条数为.

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤。

15. (2024高二下·杭州期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .再从条件①、条件②、条件③这三个条件中选择一个作为已知，使 $\text{[math]}$ 存在且唯一确定，并解决下面的问题：
条件①： $\text{[math]}$ ；条件②： $\text{[math]}$ ；条件③： $\text{[math]}$ .
注：如果选择的条件不符合要求，不给分；如果选择多个符合要求的条件分别解答，按第一个解答计分.
1. （1）求 $\text{[math]}$ 的大小，
2. （2）求 $\text{[math]}$ 的面积
答案解析收藏纠错 + 选题
16. (2024高二下·杭州期中) 已知 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 处取得极小值 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的解析式
2. （2）求 $\text{[math]}$ 在 $\text{[math]}$ 处的切线方程.
3. （3）若方程 $\text{[math]}$ 有且只有一个实数根，求k的取值范围.
答案解析收藏纠错 + 选题
17. (2024高二下·杭州期中) 已知数列 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上.
1. （1）求数列 $\text{[math]}$ 的通项公式及其前 $\text{[math]}$ 项的和 $\text{[math]}$ .
2. （2）设 $\text{[math]}$ ， $\text{[math]}$ ，证明： $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2024高二下·杭州期中) 如图，在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 是边长为2的菱形， $\text{[math]}$ 是等边三角形， $\text{[math]}$ ，点 $\text{[math]}$ 分别为 $\text{[math]}$ 和 $\text{[math]}$ 的中点
1. （1）求证： $\text{[math]}$ $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；
3. （3）求 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值.
答案解析收藏纠错 + 选题
19. (2024高二下·杭州期中) 已知椭圆 $\text{[math]}$ ： $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，左、右顶点分别为 $\text{[math]}$ ， $\text{[math]}$ ，若以 $\text{[math]}$ 圆心，1为半径的圆与以 $\text{[math]}$ 为圆心，3为半径的圆相交于A ， B两点，若椭圆E经过A ， B两点，且直线 $\text{[math]}$ ， $\text{[math]}$ 的斜率之积为 $\text{[math]}$ .
1. （1）求椭圆E的方程
2. （2）点P是直线 $\text{[math]}$ ： $\text{[math]}$ 上一动点，过点P作椭圆E的两条切线，切点分别为M ， N.
  ①求证直线 $\text{[math]}$ 恒过定点，并求出此定点.
  ②求 $\text{[math]}$ 面积的最小值.
答案解析收藏纠错 + 选题