一、单项选择题(本大题共有6小题,每题3分,共18分。)
二、填空题(本大题有6小题,每小题3分,共18分。)
-
-
8.
已知

是完全平方式,则

的值是
.
-
-
-
-
12.
(2024七下·乐平期中)
已知王强家、体育场、学校在同一直线上,下面的图象反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中

表示时间,

表示王强离家的距离.则下列结论正确的是
.(填写所有正确结论的序号)
①体育场离王强家 ②王强在体育场锻炼了
②王强在体育场锻炼了
③王强吃早餐用了 ④王强骑自行车的平均速度是
④王强骑自行车的平均速度是

三、解答题。(本大题有5小题,每小题6分,共30分)
-
-
(1)

-
(2)

(用简便方法计算)
-
-
-
-
17.
(2024七下·乐平期中)
草莓销售季节,某种植基地开发了草莓采摘无人销售方式,为方便小朋友体验,销售人员把销售的草莓数量

与销售总价

(元)之间的关系写在了下列表格中:
销售数量 | 1 | 2 | 3 | 4 | … |
销售总价 /元 /元 | 8.5 | 16.5 | 24.5 | 32.5 | … |
-
(1)
请你写出草莓的销售数量

与销售总价

(元)之间的关系式.
-
(2)
丽丽一家共摘了

草莓,应付多少钱?
四、解答题。(本大题有3小题,每小题8分,共24分)
-
-
19.
(2024七下·乐平期中)
填写下面解题过程中的推理依据:如图,

,

平分
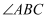
,

平分

.

(本题第(1)小题在下面的解答过程的空格内填写理由或数学式,第(2)小题要写出解题过程)
-
(1)

吗?请说明理由.
解:(1) , 理由如下:
, 理由如下:
因为 (已知),
(已知),
所以 ( ).
( ).
因为 平分
平分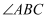 ,
,  平分
平分 (已知),
(已知),
所以 ▲ (角平分线的定义),
▲ (角平分线的定义), ▲ (角平分线的定义),
▲ (角平分线的定义),
所以 ( ).
( ).
-
(2)

与

的位置关系如何?为什么?
-
-
(1)
根据题意,将表格补充完整.
立柱根数 | 1 | 2 | 3 | 4 | 5 | … |
护栏总长度/米 | 0.2 | 3.4 |
| 9.8 |
| … |
-
(2)
在这个变化过程中,自变量、因变量各是什么?
-
(3)
设有

根立柱,护栏总长度为

米,则

与

之间的关系式是什么?
-
五、解答题。(本大题有2小题,每小题9分,共18分)
-
21.
(2024七下·乐平期中)
如图①是一个长为

、宽为

的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.

-
(1)
请用两种不同的方法表示图②中阴影部分的面积(结果不化简).
方法1:;方法2:.
-
(2)
观察图②,请写出

,

,

三个式子之间的等量关系;
-
(3)
根据(2)题中的等量关系,解决如下问题:已知

,

, 求

的值.
-
22.
(2024七下·乐平期中)
如图1,以直线

上一点

为顶点作射线

, 使

.将一个直角三角板

的直角顶点

放在直线

上的点

处,边

放在射线

上.

-
(1)

.
-
(2)
如图2,将直角三角板

绕点

按逆时针方向转动,当射线

恰好平分

时,求

的度数.
-
(3)
如图3,将直角三角板

绕点

转动,如果

始终在

的内部,试猜想

和

有怎样的数量关系,并说明理由.
六、解答题。(本大题12分)
-
-
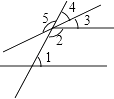
(1)
如图(1),

, 点

在

、

外部,若

,

, 则


.
-
(2)
如图(2),

, 点

在

、

内部,则

,

,

之间有何数量关系?证明你的结论;
-
(3)
在图(2)中,将直线

绕点

按逆时针方向旋转一定角度交直线

于点

, 如图(3),若

,

, 直接写出

的度数.

 B .
B .  C .
C .  D .
D . 
②王强在体育场锻炼了
④王强骑自行车的平均速度是

, 理由如下:
(已知),
( ).
平分
,
平分
(已知),
▲ (角平分线的定义),
▲ (角平分线的定义),
( ).

