一、选择题(共10小题,每小题3分,满分30分)
-
-
-
A . 2,3,4
B . 3,4,6
C . 4,6,7
D . 5,12,13
-
-
A . 对角线互相平分
B . 对角线互相垂直
C . 四个角相等
D . 四条边相等
-
A . 2
B . 3
C . 4
D . 2 
-
7.
(2024八下·中山期中)
如图,在平行四边形ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠DAE的角度为( )

A . 25°
B . 35°
C . 45°
D . 55°
-
A . 10
B . 8
C .  D . 5
D . 5
-
9.
(2024八下·中山期中)
如图,平面直角坐标系xOy中,点A,B的坐标分别是(﹣2,0)和(0,3),以A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标是( )

-
10.
(2024八下·中山期中)
如图,在平面直角坐标系中,正方形ABCD的顶点D在y轴上,A(-3,0),B(1,b),则正方形ABCD的面积为( )

A . 34
B . 25
C . 20
D . 16
二、填空题(共5小题,每小题4分,满分20分)
-
-
-
13.
(2024八下·中山期中)
如图,菱形ABCD的顶点B在x轴上,顶点C在y轴上,点A的坐标为(-4,1),点C的坐标为(0,1),则点D的坐标为
.

-
-
15.
(2024八下·中山期中)
如图,四边形ABCD与CEFG均为矩形,使得G,D,C共线,B,C,E共线,取AD中点M,连接AF,GM交于点H,若BC=EF=4,CD=CE=2,则AH=
.

三、解答题(一)(共4小题,每小题6分,共24分)
-
-
-
18.
(2024八下·中山期中)
如图,图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足BC⊥CD,现测得AB=CD=6dm,BC=3dm,AD=9dm,其中AB与BD之间由一个固定为90°的零件连接(即∠ABD=90°),通过计算说明该车是否符合安全标准.

-
四、解答题(二)(共3小题,每小题8分,共24分)
-
-
21.
(2024八下·中山期中)
如图,在四边形ABCD中, AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,连接AC.
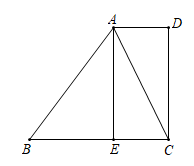
-
-
(2)
若AC平分∠DAB,AB=5,EC=2,求AE的长,
-
22.
(2024八下·中山期中)
如图,在平行四边形ABCD中,AD>AB,AE平分∠BAD,交BC于点E,过点E作EF∥AB交AD于点F.

-
-
(2)
若菱形ABEF的周长为16,∠EBA=120°,求AE的大小.
五、解答题(三)(共2小题,第23题10分,第24题12分,共22分)
-
23.
(2024八下·中山期中)
如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.

-
-
(2)
如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.
-
24.
(2024八下·中山期中)
定义:有两个相邻的内角是直角,并且有两条邻边相等的四边形称为邻等四边形.邻等四边形中,相等两邻边的夹角称为邻等角.

-
(1)
如图1,在四边形ABCD中,∠BAD=∠B=90°,对角线AC平分∠BCD,求证:四边形ABCD是邻等四边形;
-
(2)
如图2,在5×6的方格纸中,A,B,C三点均在格点上,若四边形ABCD是邻等四边形,请画出所有符合条件的格点D,并分别用D1 , D2 , D3 , …表示;
-
(3)
如图3,四边形ABCD是邻等四边形,∠A=∠B=90°,∠BCD为邻等角.若AB=8,AD=6,求邻等四边形ABCD的周长.













