如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B等于( )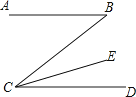

 B .
B .  C .
C .  D .
D . 

数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
如图1是一个边长为的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为a和b;图2是一个边长为a的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为
和b , 请分别写出阴影部分的面积所揭示的乘法公式:
图1;图2;
用4个全等的长和宽分别为a , b的长方形拼摆成一个如图3的正方形,请你通过计算阴影部分的面积,直接写出这三个代数式之间的等量关系.
如图4,C是线段AB上的一点,分别以AC , BC为边向两边作正方形ACDE和BCFG , 若 , 两正方形的面积和为20,求
的面积.
若 , 则
.(直接写出结果)
[问题情境]
周末,小明同学骑车去学校取书,出门匆忙,骑行一段路后,发现学生证落在同学小强家了,于是又返同学小强家中取学生,并停留了一段时间,之后再继续骑车向学校出发,最后到达学校。
[学以致用]
聪明的小明同学,以所用的时间(分钟)为横轴,以离家的距离s(米)为纵轴建立平面直角坐标系,对周末活动做以下示意图,并受到数学老师夸赞.

[解决问题]
根据图中提供的信息回答下列问题:
和
是两个都含有
角的大小不同的直角三角板.

当两个三角板如图(1)所示的位置摆放时,D、B , C在同一直线上,连接AD、CE , 请证明: .
当三角板ABC保持不动时,将三角板DBE绕点B顺时针旋转到如图(2)所示的位置,判断AD与CE的数量关系和位置关系,并说明理由.
如图(3),在四边形ABCD中, , 连接AC , BD ,
, A到直线CD的距离为7,请求出
的面积.