一、选择题(本题共10小题,每小题3分,共30分.每小题只有一个选项符合题意)
-
-
2.
(2024七下·成都期末)
“墙角数枝梅,凌寒独自开.遥知不是雪,为有暗香来.”出自宋代诗人王安石的《梅花》.梅花的花粉直径约为0.000036m,用科学记数法表示为

, 则
n的值为( )
A . -4
B . -5
C . 4
D . 5
-
-
A . 55°
B . 45°
C . 35°
D . 30°
-
-
6.
(2024·厚街模拟)
单项式

表示球的表面积,其中

表示圆周率,
r表示球的半径.下列说法中,正确的是( )
A . 系数是4,次数是2
B . 系数是4,次数是3
C . 系数是 , 次数是3
D . 系数是
, 次数是3
D . 系数是 , 次数是2
, 次数是2
-
-
8.
(2024·厚街模拟)
东莞国贸大厦某店一天中卖出某种品牌的休闲鞋16双,它们的尺码与销售量如表所示:
鞋的尺码/cm | 25 | 25.5 | 26 | 26.5 | 27 |
销售量/双 | 2 | 3 | 4 | 4 | 3 |
则这16双鞋的尺码组成的数据中,中位数是( )
A . 25.5
B . 26
C . 26.5
D . 27
-
-
10.
(2024·厚街模拟)
如图,在

中,

,

,

, 将

绕点
A逆时针旋转得到

, 使点

落在
AB边上,连结

, 则

的值为( )

二、填空题(本题共5小题,每小题3分,共15分。)
-
-
-
-
14.
(2024·厚街模拟)
在一个不透明的袋子中放有若干个球,其中有5个白球,其余是黄球,这些球除颜色外完全相同.每次把球充分揽匀后,任意摸出一个球记下颜色,再放回袋子通过大量重复试验后,发现摸到白球的频率稳定在0.2左右,则黄球的个数约是
.
-
15.
(2024·厚街模拟)
已知正三角形
ABC的边长为2cm,若以
AC为边作一个正方形
ACDE , 则点
B到边
DE距离为
cm.
三、解答题(一)(本题共2小题,每小题5分,共10分。)
四、解答题(二)(本题共3小题,每小题7分,共21分。)
-
-
(1)
用尺规作图法作AB的垂直平分线DE , 分别交AC、AB于点D和点E , (保留作图痕迹,不要求写作法);
-
(2)
在(1)的条件下,连接
BD , 当

时,求
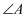
的度数.
-
19.
(2024·厚街模拟)
2021年7月1日是建党100周年纪念日,在本月日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为48,求这个最小数(请用方程知识解答).

-
五、解答题(三)(本题共3小题,每小题8分,共24分。)
-
21.
(2024·厚街模拟)
综合与探究
【阅读理解】
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,解决问题的策略一般都是进行一定的转化,其中“作差法”就是常用的方法之一.作差法:就是通过作差、变形,利用差的符号确定它们的大小,即要比较代数式A、B的大小,只要算 的值,若
的值,若 , 则
, 则 ;若
;若 , 则
, 则 ;若
;若 , 则
, 则 .
.
【知识运用】
-
-
(2)
试比较与

与

的大小,并说明理由;
-
-
22.
(2024·厚街模拟)
在贯彻落实“五育并举”的工作中,某校开设了五个社团活动:传统国学(
A)、科技兴趣(
B)、民族体育(
C)、艺术鉴赏(
D)、劳技实践(
E),每个学生每个学期只参加一个社团活动.为了了解本学期学生参加社团活动的情况,学校随机抽取了若干名学生进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.请根据统计图提供的信息,解答下列问题:

-
-
(2)
在扇形统计图中,传统国学(A)对应扇形的圆心角度数是;
-
(3)
若该校有2700名学生,请估算本学期参加艺术鉴赏(D)活动的学生人数;
-
(4)
若小明和小亮可从这五个社团活动中任选一个参加,请直接写出两人恰好选择同一个社团的概率.
-
23.
(2024·厚街模拟)
如图,矩形
OABC的顶点
A、
C分别在
x、
y轴的正半轴上,点
D为对角线
OB的中点,点

在边
AB上,反比例函数

在第一象限内的图象经过点
D、
E , 且

.

-
(1)
①直接写出边
AB的长为
▲ .
②求反比例函数的解析式.
-
(2)
若反比例函数的图象与矩形的边BC交于点F , 将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G , 求线段OG的长.
六、解答题(四)(本题共2小题,每小题10分,共20分。)
-
-
(1)
若

, 求证:
BD是

的直径;
-
(2)
求证:直线
AF是

的切线;
-
(3)
若

,

, 求
ED的长.
-
25.
(2024·厚街模拟)
综合应用.
已知抛物线 与x轴交于
与x轴交于 ,
,  两点,与y轴交于点C , 点P是抛物线一动点.
两点,与y轴交于点C , 点P是抛物线一动点.

-
-
(2)
如图1,当点
P是第一象限内且在
BC上方的动点,连接
AP , 交
BC于点
D , 若

, 求点
P的坐标;
-
(3)
如图2,若点
P在直线
BC下方的抛物线上,过点
P作

, 垂足为
Q , 求

的最大值.
 B .
B .  C .
C .  D .
D . 

的值,若
, 则
;若
, 则
;若
, 则
.
; ②
;
得到如图(2)所示的长方形,此长方形的面积为
;将正方形的边长增加a , 得到如图(3)所示的大正方形,此正方形的面积为
. 请先判断
与
的大小关系,并说明理由.

