广东省深圳市2024届高三下学期三模数学试题

更新时间：2024-07-09 浏览次数：34 类型：高考模拟

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2024·深圳模拟) 已知全集 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . {4} C . {5} D . {1，2}

答案解析收藏纠错 + 选题
2. (2024·深圳模拟) 若复数z的实部大于0，且 $\text{[math]}$ ，则z=（）

A . 1-2i B . -1-2i C . -1+2i D . 1+2i

答案解析收藏纠错 + 选题
3. (2024·深圳模拟) 已知向量 $\text{[math]}$ 是平面上两个不共线的单位向量，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . A、B、C三点共线 B . A、B、D三点共线 C . A、C、D三点共线 D . B、C、D三点共线

答案解析收藏纠错 + 选题
4. (2024高三下·深圳模拟) 已知数列 $\text{[math]}$ 满足： $\text{[math]}$ ，且数列 $\text{[math]}$ 为等差数列，则 $\text{[math]}$ （）

A . 10 B . 40 C . 100 D . 103

答案解析收藏纠错 + 选题
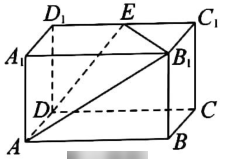
5. (2024·深圳模拟) 如图，已知长方体 $\text{[math]}$ 的体积为 $\text{[math]}$ 是棱 $\text{[math]}$ 的中点，平面 $\text{[math]}$ 将长方体分割成两部分，则体积较小的一部分的体积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·深圳模拟) 已知椭圆 $\text{[math]}$ ，直线 $\text{[math]}$ 与E交于A、B两点，且 $\text{[math]}$ ．则椭圆E的离心率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高三下·深圳模拟) 某羽毛球俱乐部，安排男女选手各6名参加三场双打表演赛（一场为男双，一场为女双，一场为男女混双），每名选手只参加1场表演赛，则所有不同的安排方法有（）

A . 2025种 B . 4050种 C . 8100种 D . 16200种

答案解析收藏纠错 + 选题
8. (2024·深圳模拟) 设函数 $\text{[math]}$ ．若实数 $\text{[math]}$ 使得 $\text{[math]}$ 对任意 $\text{[math]}$ 恒成立，则 $\text{[math]}$ （）

A . -1 B . 0 C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. (2024高三下·深圳模拟) 平行六面体中，各个表面的直角个数之和可能为（）

A . 0 B . 4 C . 8 D . 16

答案解析收藏纠错 + 选题
10. (2024高三下·深圳模拟) 已知函数 $\text{[math]}$ 有最小正零点 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 在 $\text{[math]}$ 上单调，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024·深圳模拟) 如图，三棱台 $\text{[math]}$ 的底面ABC为锐角三角形，点D ， H ， E分别为棱 $\text{[math]}$ ， BC，的中点，且 $\text{[math]}$ ， AC+AB=4；侧面 $\text{[math]}$ 为垂直于底面的等腰梯形，若该三棱台的体积最大值为 $\text{[math]}$ ，则下列说法可能但不一定正确的是（）

A . 该三棱台的体积最小值为 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分．

12. (2024高三下·深圳模拟) 写出函数 $\text{[math]}$ 的一条斜率为正的切线方程：.

答案解析收藏纠错 + 选题
13. (2024·深圳模拟) 两个连续随机变量X ， Y满足 $\text{[math]}$ ，且 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2024·深圳模拟) 双曲线 $\text{[math]}$ 的左右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，以实轴为直径作圆O ，过圆O上一点E作圆O的切线交双曲线的渐近线于A ， B两点（B在第一象限），若 $\text{[math]}$ ， $\text{[math]}$ 与一条渐近线垂直，则双曲线的离心率为.

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，第15小题13分，第16、17小题15分，第18、19小题17分，共77分．解答应写出文字说明、证明过程或演算步骤．

15. (2024高三下·深圳模拟) 数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，
1. （1）求数列 $\text{[math]}$ 的通项公式；
2. （2）数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，且满足 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
16. (2024·深圳模拟) 如图，一个质点在随机外力的作用下，从数轴点1的位置出发，每隔向左或向右移动一个单位，设每次向右移动的概率为p(0<p<1).
1. （1）当 $\text{[math]}$ 时，求5s后质点移动到点O的位置的概率，
2. （2）记3s后质点的位置对应的数为X ，若随机变量X的期望E(X)>0，求p的取值范围.
答案解析收藏纠错 + 选题
17. (2024·深圳模拟) 如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PA=PB= $\text{[math]}$ ，点M在PD上，点N为BC的中点，且PB//平面MAC.
1. （1）证明：CM//平面PAN ，
2. （2）若PC=3，求平面PAN与平面MAC夹角的余弦值.
答案解析收藏纠错 + 选题
18. (2024高三下·深圳模拟) 已知双曲线 $\text{[math]}$ 经过椭圆 $\text{[math]}$ 的左、右焦点 $\text{[math]}$ ， $\text{[math]}$ 设 $\text{[math]}$ ， $\text{[math]}$ 的离心率分别为 $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的方程，
2. （2）设P为 $\text{[math]}$ 上一点，且在第一象限内，若直线 $\text{[math]}$ 与 $\text{[math]}$ 交于A ， B两点，直线 $\text{[math]}$ 与 $\text{[math]}$ 交于C ， D两点，设AB ， CD的中点分别为M ， N ，记直线MN的斜率为k ，当k取最小值时，求点P的坐标.
答案解析收藏纠错 + 选题
19. (2024·深圳模拟) 英国数学家泰勒发现的泰勒公式有如下特殊形式：当 $\text{[math]}$ 在x=0处的 $\text{[math]}$ 阶导数都存在时， $\text{[math]}$ .注： $\text{[math]}$ 表示 $\text{[math]}$ 的2阶导数，即为 $\text{[math]}$ 的导数， $\text{[math]}$ 表示 $\text{[math]}$ 的n阶导数，该公式也称麦克劳林公式.
1. （1）根据该公式估算 $\text{[math]}$ 的值，精确到小数点后两位，
2. （2）由该公式可得： $\text{[math]}$ .当 $\text{[math]}$ 时，试比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小，并给出证明，
3. （3）设 $\text{[math]}$ ，证明： $\text{[math]}$ .
答案解析收藏纠错 + 选题