一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的.)
-
1.
(2024·南山模拟)
古钱币是我国悠久的历史文化遗产,以下是在《中国古代钱币》特种邮票中选取的部分图形,下列既是轴对称图形又是中心对称图形的是( )
-
-
-
-
5.
(2024·南山模拟)
如上图,点B、F、C、E都在一条直线上,

, 添加下列一个条件后,仍无法判断

的是( )

-
6.
(2024·南山模拟)
《生日歌》是我们熟悉的歌曲,以下是摘自生日歌简谱的部分旋律,当中出现的音符的中位数是( )

A . 1
B . 2
C . 5
D . 6
-
-
8.
(2024·南山模拟)
某机械厂今年生产零件50万个,计划明后两年共生产零件132万个,设该厂每年的平均增长率为

, 那么

满足方程( )
-
-
10.
(2024·南山模拟)
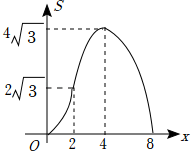
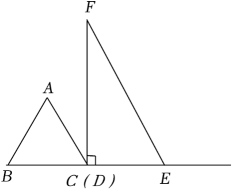
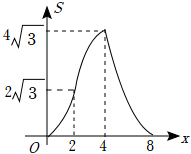
如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
二、填空题(本大题共5小题,每小题3分,共15分)
-
-
-
-
14.
(2024·南山模拟)
如图,某品牌扫地机器人的形状是“莱洛三角形”,它的三“边”分别是以等边三角形的三个顶点为圆心,边长为半径的三段圆弧.若该等边三角形的边长为3,则这个“莱洛三角形”的周长是
.

-
15.
(2024·南山模拟)
如图,在

中,

, 点

是边BC上一动点(不与B、C重合),

DE交AC于点

, 且

, 则线段

的最大值为
.

三、解答题(本大题共7小题,共55分)
-
-
-
18.
(2024·南山模拟)
劳动教育具有树德、增智、强体、育美的综合育人价值,有利于学生树立正确的劳动价值观.某学校为了解学生参加家务劳动的情况,随机抽取了

名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中己有信息,解答下列问题:

劳动时间t(单位:小时) | 频数 |

| 12 |
1≤t<1.5 | a |

| 26 |

| 16 |

| 4 |
-
(1)

,

;
-
(2)
若该校学生有640人,试估计劳动时间在

范围的学生有多少人?
-
(3)
劳动时间在

范围的4名学生中有男生2名,女生2名,学校准备从中任意抽取2名交流劳动感受,求抽取的2名学生恰好是二名女生的概率.
-
19.
(2024·南山模拟)
我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购头甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.
-
-
(2)
根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的

, 应如何购买才能使总费用最少?并求出最少费用.
-
20.
(2024·南山模拟)
已知,如图,AB是

的直径,点

为

上一点,

于点

, 交

于点E,AE与BC交于点

, 点

为OE的延长线上一点,且

.

-
(1)
求证:BD是

的切线;
-
(2)
若

的半径为

, 求BH的长.
-
21.
(2024·南山模拟)
【项目式学习】根据以下素材,探索完成任务.
绿化带灌溉车的操作方案 |
素材1 | 一辆绿化带灌溉车正在作业,水从喷水口喷出,水流的上下两边缘可以抽象为两条抛物线的一部分:喷水口离开地面高1.6米,上边缘抛物线最高点离喷水口的水平距离为3米,高出喷水口0.9米,下边缘水流形状与上边缘相同,且喷水口是最高点. | 
|
素材2 | 路边的绿化带宽4米 | |
素材3 | 绿化带正中间种植了行道树,为了防治病虫害、增加行道树的成活率,园林工人给树木“打针”,针一般打在离地面1.5米到2米的高度(包含端点). | 
|
问题解决 |
任务1 | 确定上边缘水流形状 | 建立如图所示直角坐标系,求上边缘抛物线的函数表达式 
|
任务2 | 探究灌溉范围 | 灌溉车行驶过程中喷出的水能浇灌到整个绿化带吗?请说明理由 |
任务3 | 拟定设计方案 | 灌溉时,发现水流的上下两边缘冲击力最强,喷到针筒容易造成针筒脱落,那么请问在满足最大灌溉面积的前提下对行道树“打针”是否有影响,并说明理由;若你认为有影响,请给出具体的“打针”范围. |
-
22.
(2024·南山模拟)
已知:如图,在四边形

和

中,

,

,点C在

上,

,

,

,延长

交

于点M,点P从点A出发,沿

方向匀速运动,速度为

;同时,点Q从点M出发,沿

方向匀速运动,速度为

,过点

作

于点H,交

于点G.设运动时间为

.

解答下列问题:
-
(1)
当

为何值时,点M在线段

的垂直平分线上?
-
(2)
连接PQ,作

于点N,当四边形

为矩形时,求t的值;
-
(3)
连接

,

,设四边形

的面积为

,求S与t的函数关系式;
-
(4)
点P在运动过程中,是否存在某一时刻t,使点P在

的平分线上?若存在,求出t的值;若不存在,请说明理由.
 B .
B .  C .
C . 
 B .
B .  C .
C .  D .
D . 


 B .
B . 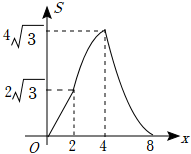 C .
C . 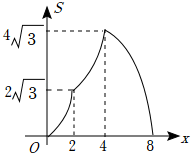 D .
D .