广东省汕头市澄海区2023-2024学年七年级下学期数学期末...

更新时间：2024-08-29 浏览次数：4 类型：期末考试

一、选择题（本大题共10小题，每小题3分，共30分）

1. (2024七下·澄海期末) 在实数0， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，无理数的个数是( )

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
2. (2024七下·澄海期末) 下列各组数中互为相反数的是( )

A . $\text{[math]}$ 与 $\text{[math]}$ B . $\text{[math]}$ 与 $\text{[math]}$ C . 2与 $\text{[math]}$ D . $\text{[math]}$ 与 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·澄海期末) 如图，直线AB与CD相交于点O ，若∠1=3∠2，则∠3的度数为( )

A . 30° B . 40° C . 45° D . 60°

答案解析收藏纠错 + 选题
4. (2024七下·澄海期末) 若点A(a ， 3)在y轴上，则点P( $\text{[math]}$ ， $\text{[math]}$ )的坐标为( )

A . （-3，-2） B . （-3，2） C . （3，2） D . （3，-2）

答案解析收藏纠错 + 选题
5. (2024七下·澄海期末) 以方程组 $\text{[math]}$ 的解为坐标的点（x ， y）在平面直角坐标系中的位置是( )

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
6. (2024七下·澄海期末) 不等式 $\text{[math]}$ 的正整数解有( )

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
7. (2024七下·澄海期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则x与y的大小关系为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
8. (2024七下·澄海期末) 为确保信息安全，信息需要加密传输，发送方将明文加密传输给接收方，接收方收到密文后解密还原为明文，已知某种加密规则为：明文a ， b对应的密文为a-2b ， 2a+b ，例如1，2对应的密文是-3，4．当接收方收到的密文是1，7时，解密得到的明文是( )

A . -1，1 B . 1，1 C . 1，3 D . 3，1

答案解析收藏纠错 + 选题
9. (2024七下·澄海期末) 如图，直线AB∥CD∥EF ，点O在直线EF上，下列结论正确的是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·澄海期末) 如图，AE $\text{[math]}$ CF ， ∠ACF的平分线交AE于点B ， G是CF上的一点，∠GBE的平分线交CF于点D ，且BD⊥BC ，下列结论：①BC平分∠ABG；②AC $\text{[math]}$ BG；③与∠DBE互余的角有2个；④若 $\text{[math]}$ ，则∠BDF=180°− $\text{[math]}$ ，其中正确的是( )

A . ①② B . ②③④ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

11. (2024七下·澄海期末) 比较大小： $\text{[math]}$ 4（填“＞”、“＜”或“＝”）．

答案解析收藏纠错 + 选题
12. (2024七下·澄海期末) 已知点P( $\text{[math]}$ ， $\text{[math]}$ )在平面直角坐标系中第一象限内，若点P到x轴的距离为3，则点P到y轴的距离为．

答案解析收藏纠错 + 选题
13. (2024七下·澄海期末) 如图，在△ABC中，∠C＝90°，EF∥AB ， ∠B＝50°，则∠1的度数为．

答案解析收藏纠错 + 选题
14. (2024七下·澄海期末) 已知关于x的不等式 $\text{[math]}$ 的解集在数轴上的表示如图，则a的值是．

答案解析收藏纠错 + 选题
15. (2024七下·澄海期末) 某班女生的体育测试被分成了三组，统计情况如表所示，则表中m的值是.

第一组
第二组
第三组
频数
7
8
M
频率
p
q
25%

答案解析收藏纠错 + 选题
16. (2024七下·澄海期末) 如图，七个相同的小长方形组成一个大长方形 $\text{[math]}$ ，若 $\text{[math]}$ ，则长方形 $\text{[math]}$ 的周长为.

答案解析收藏纠错 + 选题

三、解答题（一）（本大题共3小题，每小题6分，共18分）

17. (2024七下·澄海期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024七下·澄海期末) 解不等式组： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2024七下·澄海期末) 完成下面推理过程，并在括号内填上推理依据．
如图，已知：AB//EF ， EP⊥EQ ， ∠EQC+∠APE=90°，求证：AB//CD ．
证明：∵AB//EF ，
∴∠APE=     ( )，
∵EP⊥EQ ，
∴∠QEF+∠PEF=90°，
∴∠APE+∠QEF=90°，
∵∠EQC+∠APE=90°，
∴∠EQC=     ，
∴EF//    ( )，
∴AB//CD( )．

答案解析收藏纠错 + 选题

四、解答题（二）（本大题共3小题，每小题8分，共24分）

20. (2024七下·澄海期末) 如图，方格纸中每个小方格都是边长为1个单位长度的正方形，若学校位置坐标为A(2，1)，图书馆位置坐标为B(-1，-2)，解答以下问题：
1. （1）在图中找出坐标系的原点，并建立平面直角坐标系；
2. （2）若体育馆位置坐标为C(1，-3)，请在坐标系中标出体育馆的位置；
3. （3）在(2)的条件下，顺次连接学校、图书馆、体育馆，得到△ABC ，求△ABC的面积．
答案解析收藏纠错 + 选题
21. (2024七下·澄海期末) 若关于x、y的二元一次方程组 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
2. （2）若方程组的解 $\text{[math]}$ 与 $\text{[math]}$ 满足条件 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
22. (2024七下·澄海期末) 为庆祝“六一”儿童节，某商场全部商品打折出售．打折前，买60件A商品和30件B商品用了1080元，买50件A商品和10件B商品用了840元；打折后，买500件A商品和400件B商品用了8640元．求该商品打几折？

答案解析收藏纠错 + 选题

五、解答题（三）（本大题共3小题，每小题10分，共30分）

23. (2024七下·澄海期末) 阅读理解，并解决问题：
若 $\text{[math]}$ 为实数，则 $\text{[math]}$ 表示不大于 $\text{[math]}$ 的最大整数，例如 $\text{[math]}$ ， $\text{[math]}$ 等． $\text{[math]}$ 是大于 $\text{[math]}$ 的最小整数，对任意的实数 $\text{[math]}$ 都满足不等式 $\text{[math]}$ --------①．
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）利用题中不等式①，求出满足 $\text{[math]}$ 的所有解．
答案解析收藏纠错 + 选题
24. (2024七下·澄海期末) 如图，已知点B、C在线段AD的异侧，连接AB、CD ，点E、F分别是线段AB、CD上的点，连接CE、BF ，分别与AD交于点G、H ，且 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
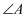
3. （3）在（2）的条件下，若∠BFC=2∠A ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
25. (2024七下·澄海期末) 如图，在平面直角坐标系中，已知点A、B的坐标分别是（a ， 0）、（b ， 0），且a、b满足方程组 $\text{[math]}$ ， C为y轴正半轴上一点，且 $\text{[math]}$ ．
1. （1）求A、B、C三点的坐标；
2. （2）是否存在点P（t ， t），使 $\text{[math]}$ ？若存在，请求出P点坐标；若不存在，请说明理由；
3. （3）若M是AC的中点，N是BC上一点，CN=2BN ，连结AN、BM ， AN与BM交于点D ，连接CD ，求四边形CMDN的面积．
答案解析收藏纠错 + 选题