一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)
-
-
-
-
-
5.
(2024高三上·广东月考)
在杭州亚运会上,我国选手盛李豪夺得射击第一枚金牌,他射击的方向向量

, 另一名选手余浩楠射击的方向向量

, 若

, 则

( )
-
6.
(2024高三上·广东月考)
研究数据表明,某校高中生的数学成绩与物理成绩、物理成绩与化学成绩均有正相关关系.现从该校抽取某班50位同学的数学、物理、化学三科成绩作为样本,设数学、物理、化学成绩分别为变量x,y,z若x,y的样本相关系数为

, y,z的样本相关系数为

, 则x、z的样本相关系数的最大值为( )
附:相关系数
-
-
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分)
-
-
A . 若 平面
平面 , 则点P的轨迹长度为
, 则点P的轨迹长度为 B . 若
B . 若 平面
平面 , 则三棱锥
, 则三棱锥 的体积为定值
C . 若
的体积为定值
C . 若 , 则点P的轨迹长度为
, 则点P的轨迹长度为 D . 若P是棱
D . 若P是棱 的中点,则三棱锥
的中点,则三棱锥 的外接球的表面积是
的外接球的表面积是
-
三、填空题(本大题共3小题,每小题5分,共15分)
四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤)
-
-
(1)
求角

;
-
(2)
若

为锐角三角形,且

, 求a的取值范围.
-
16.
(2024高三上·广东月考)
在如图所示的实验装置中,两个正方形框架

,

的边长都是1,且他们所在的平面互相垂直,活动弹子

,

分别在正方形对角线

和

上移动,且
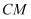
和

的长度保持相等,及


-
(1)
求

的长;
-
(2)

为何值时,

的长最小,最小值是多少?
-
(3)
当

的长最小时,求平面

与平面

的夹角的余弦值.
-
17.
(2024高三上·广东月考)
传球是排球运动中最基本、最重要的一项技术.传球是由准备姿势、迎球、击球、手型、用力5个动作部分组成.其中较难掌握的是触球时的手型,因为触球时手型正确与否直接影响手控制球的能力和传球的准确性,对初学者来说掌握了正确手型才能保证正确击球点和较好的运用手指,手腕的弹力.从小张、小胡、小郭、小李、小陈这5人中随机地抽取三个人去做传球训练.训练规则是确定一人第一次将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,每次必须将球传出.
-
(1)
记小胡、小李、小陈这三人中被抽到的人数为随机变量

, 求

的分布列;
-
(2)
若刚好抽到小胡、小李、小陈三个人相互做传球训练,且第1次由小胡将球传出,记

次传球后球在小胡手中的概率为

.
①直接写出 的值;
的值;
②求 与
与 的关系式
的关系式 , 并求
, 并求 .
.
-
-
(1)
求函数

的值域;
-
-
(3)
当

时,函数

的值域为

, 求正数

的取值范围.
-
-
(1)
求双曲线

的标准方程;
-
(2)
双曲线的左、右顶点分别为

, 过点

作与

轴不重合的直线

与

交于

两点,直线

与

交于点S,直线

与

交于点

.
(i)设直线 的斜率为
的斜率为 , 直线
, 直线 的斜率为
的斜率为 , 若
, 若 , 求
, 求 的值;
的值;
(ii)求 的面积的取值范围.
的面积的取值范围.
的值;
与
的关系式
, 并求
.
的斜率为
, 直线
的斜率为
, 若
, 求
的值;
的面积的取值范围.