一、选择题(本题共10小题,每小题3分,共30分)在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题纸上.
-
1.
(2024八上·启东期中)
为估计池塘两岸A、B间的距离,如图,小明在池塘一侧选取了一点O,测得OA=16m,OB=12m,那么AB的距离不可能是 ( )

A . 5m
B . 15m
C . 20m
D . 30m
-
2.
(2024八上·启东期中)
八角帽又称“红军帽”,是红军的象征,也是中国工农红军军服佩饰最显眼的部分之一,其帽顶近似正八边形.正八边形的一个内角的大小为( )

-
-
4.
(2024八上·南宁开学考)
数学中有许多精美的曲线,以下是“悬链线”、“黄金螺旋线”、“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
-
5.
(2024八上·启东期中)
已知

, 求作射线

, 使

平分

, 那么作法的合理顺序是( )
①作射线 ;
;
②在射线 和
和 上分别截取
上分别截取 , 使
, 使 ;
;
③分别以D、E为圆心,大于 的长为半径在
的长为半径在 内作弧,两弧交于点C.
内作弧,两弧交于点C.

A . ①②③
B . ②①③
C . ②③①
D . ③①②
-
6.
(2024八上·启东期中)
如图,在△ABC中,∠C=90°,AC=4,DC

AD,BD平分∠ABC,则点D到AB的距离等于( )

A . 1
B .  C . 2
D .
C . 2
D . 
-
A . 4个
B . 3个
C . 2个
D . 1个
-
8.
(2024八上·启东期中)
如图,网格中的每个小正方形的顶点称作格点,图中A、B在格点上,则图中满足△ABC为等腰三角形的格点C的个数为( )

A . 7
B . 8
C . 9
D . 10
-
9.
(2024八上·启东期中)
如图,在

中,

,

为

的角平分线.

与

相交于点F,

平分

, 有下列四个结论:①

;②

;③

;④若

,

. 其中正确的是( )

A . ①③
B . ②③④
C . ①③④
D . ①②③④
-
10.
(2024八上·山海关期末)
如图,

的两条高

与

交于点

,

,

. 点

在射线

上,且

, 动点

从点

出发,沿线段

以每秒

个单位长度的速度向终点

运动,同时动点

从点

出发,沿射线

以每秒

个单位长度的速度运动,当点

到达点

时,

,

两点同时停止运动,设运动时间为

秒,当

与

全等时,则

的值为( )

A .  秒
B .
秒
B .  秒
C .
秒
C .  秒或
秒或 秒
D .
秒
D .  秒或
秒或 秒
秒
二、填空题(本题共8小题,第11~12题每小题3分,第13~18题每小题4分,共30分)不需写出解答过程,把最后结果填在答题纸对应的位置上.
-
-
-
-
-
-
-
17.
(2024八上·乌鲁木齐期中)
如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是
°.

-
18.
(2024八上·启东期中)
如果两条线段将一个三角形分割成3个小等腰三角形,我们把这两条线段叫做这个三角形的“优美线”.在

中,

,

和

是

的“优美线”,点D在

边上,点E在

边上,且

,

, 则
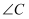
的度数为
.
三、解答题(本题共8小题,共90分)解答时应写出文字说明、证明过程或演算步骤.请在答题纸对应的位置和区域内解答.
-
-
-
(1)
作

关于x轴的对称图形

, (其中A、B、C的对称点分别是D、E、F);并写出点D坐标;
-
(2)
P为x轴上一点,请在图中面出使

的周长最小时的点P,并直接写出此时点P的坐标.
-
-
-
-
(1)
若

, 求

的度数;
-
(2)

与

相等吗?请说明理由.
-
-
-
-
(3)
通过以上的探索过程,请根据图

与图

分别写出

与

,
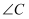
之间的数量关系,并说明理由.
-
-
(1)
如图1,当点D在线段

上(不与点A,C重合)时,求证:

;
-
(2)
当点D在线段

或线段

延长线上时,

与

有怎样的数量关系?写出你的猜想,并在图2和图3中选择一种情况给予证明.
-
-
-
(2)
用等式写出

、

、

之间的数量关系,并给出证明;
-
(3)
如果把作

的平分线

, 改为作

的外角

的平分线

, 其他条件不变,直接用等式写出

、

、

之间的数量关系.


 C .
C .  D .
D . 



