二次函数图象与性质—浙教版数学九（上）知识点训练

更新时间：2024-11-26 浏览次数：8 类型：复习试卷

一、基础夯实

1. (2024九上·鄞州期中) 下列二次函数的图象中，顶点在第二象限的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·长兴期中) 二次函数y= $\text{[math]}$ 的图象向右平移3个单位，向下平移2个单位，得到新的图象的函数表达式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·浙江期中) 已知点（2，y₁），（1，y₂），（－1，y₃）在抛物线y＝－x²＋2x＋m上，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·浙江期中) 二次函数y＝ax²＋bx＋c的图象如图所示，则点（a，b＋c）位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
5. (2024九上·浙江期中) 对于抛物线y＝3（x+2）²﹣1，下列判断不正确的是（）

A . 抛物线的顶点坐标为（﹣2，﹣1） B . 把抛物线向右平移1个单位，再向上平移2个单位，得到抛物线y＝3（x+1）²+1 C . 当x＞﹣2时，y随x的增大而增大 D . 若点A（2，y₁），B（﹣3，y₂）在抛物上，则y₁＜y₂

答案解析收藏纠错 + 选题
6. (2024九上·浙江期中) 若－1≤x≤m时，函数y＝(x－2)²＋1的最大值为17，则m＝．

答案解析收藏纠错 + 选题
7. (2024九上·诸暨月考) 已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ 和 $\text{[math]}$ ．若 $\text{[math]}$ ，则m的取值范围是．

答案解析收藏纠错 + 选题
8. (2024九上·义乌月考) 已知二次函数经过点 $\text{[math]}$ ， $\text{[math]}$ ，且最大值为 $\text{[math]}$ ．
1. （1）求二次函数的解析式；
2. （2）在平面直角坐标系 $\text{[math]}$ 中，画出二次函数的图象；
3. （3）当 $\text{[math]}$ 时，结合函数图象，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
9. (2024九上·宁波期中) 已知二次函数的解析式为 $\text{[math]}$ ，其中 $\text{[math]}$ .
1. （1）若点 $\text{[math]}$ 在该函数图象上，求这个二次函数的解析式.
2. （2）若 $\text{[math]}$ 是二次函数图象上两个不同的点；当 $\text{[math]}$ 时， $\text{[math]}$ ，求 $\text{[math]}$ 的值.
3. （3）若该二次函数图象过点 $\text{[math]}$ ，且当 $\text{[math]}$ 时 $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
10. (2024九上·温州开学考) 已知抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ 与 $\text{[math]}$ ．
1. （1）求该抛物线的解析式及它的对称轴．
2. （2）点 $\text{[math]}$ 在该抛物线上，求m的值．
3. （3）当函数值 $\text{[math]}$ 时，请直接写出自变量x的取值范围______．
4. （4）当 $\text{[math]}$ 时，请直接写出函数y的取值范围______．
答案解析收藏纠错 + 选题

二、能力提升

11. (2023九上·义乌月考) 如图，抛物线y＝﹣x²+2x+m+1交x轴于点A（a ， 0）和B（b ， 0），交y轴于点C ，抛物线的顶点为D ，下列四个命题：①当x＞0时，y＞0； ②若a＝﹣1，则b＝4；
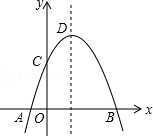
③抛物线上有两点P（x₁ ， y₁）和Q（x₂ ， y₂），若x₁＜1＜x₂ ，且x₁+x₂＞2，则y₁＞y₂；
④点C关于抛物线对称轴的对称点为E ，点G ， F分别在x轴和y轴上，当m＝2时，四边形EDFG周长的最小值为 $\text{[math]}$ ．其中真命题的序号是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
12. (2023九上·拱墅竞赛) 设函数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．直线x＝b的图象与函数y₁ ， y₂ ， y₃的图象分别交于点A（b ， c₁），B（b ， c₂），C（b ， c₃），（）

A . 若b＜a₁＜a₂＜a₃ ，则c₂＜c₃＜c₁ B . 若a₁＜b＜a₂＜a₃ ，则c₁＜c₂＜c₃ C . 若a₁＜a₂＜b＜a₃ ，则c₃＜c₂＜c₁ D . 若a₁＜a₂＜a₃＜b ，则c₃＜c₂＜c₁

答案解析收藏纠错 + 选题
13. (2023九上·义乌月考) 已知二次函数 $\text{[math]}$ （ $\text{[math]}$ ），经过点P（ $\text{[math]}$ ， 12）．当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围为 $\text{[math]}$ ．则如下四个值中有可能为 $\text{[math]}$ 的是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
14. (2023九上·期中) 二次函数 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 是常数，且 $\text{[math]}$ 的自变量 $\text{[math]}$ 与函数值 $\text{[math]}$ 的部分对应值如下表：
x
…
-1
0
1
2
…
y … m 2 2 n …
且当 $\text{[math]}$ 时，对应的函数值 $\text{[math]}$ 有以下结论： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ 关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的负实数根在 $\text{[math]}$ 和 $\text{[math]}$ 之间； $\text{[math]}$ 和 $\text{[math]}$ 在该二次函数的图象上，则当实数 $\text{[math]}$ 时， $\text{[math]}$ ．
其中正确的结论是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2024九上·浙江期中) 若抛物线和两坐标轴的交点分别为(0，2)，(m，0)，(m+6，0)，当0<x< $\text{[math]}$ m+2时，总有y>2，则m的取值范围是．

答案解析收藏纠错 + 选题
16. (2024九下·凉州模拟) 在平面直角坐标系中， $\text{[math]}$ 为坐标原点，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交抛物线于点 $\text{[math]}$ ，抛物线顶点为 $\text{[math]}$ ．若直线 $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
17. (2024九上·浙江期中) 已知二次函数y＝ax2＋bx＋3（a≠0，b是实数）图象经过四点：（－1，m），（1，n），（2，3），（4，p）．
1. （1）若m＝4，①求二次函数的表达式；②已知x≤2k－3时，y随x的增大而减小，求k的最大值．
2. （2）若m，n，p这三个实数中，有且只有一个是负数，求a的取值范围．
答案解析收藏纠错 + 选题
18. (2024九上·杭州月考)
1. （1）【问题初探】
  综合与实践数学活动课上，张老师给出了一个问题：
  已知二次函数y＝x²+2x－3，当－2≤x≤2时，y的取值范围为；
  ①小伟同学经过分析后，将原二次函数配方成y＝a(x－h)²+k
  形式，确定抛物线对称轴为直线x＝h ，通过－2、h和2的大小
  关系，分别确定了最大值和最小值，进而求出y的取值范围；
  ②小军同学画出如图的函数图象，通过观察图象确定了y的取值范围；请你根据上述两名同学的分析写出y的取值范围是；
2. （2）【类比分析】
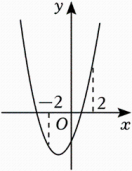
  张老师发现两名同学分别从“数”和“形”的角度分析、解决问题，为了让同学们更好感悟“数形结合”思想，张老师将前面问题变式为下面问题，请你解答：已知二次函数y＝－x²+2x－3，当－2≤x≤2时，求y的取值范围；
3. （3）【学以致用】
  已知二次函数y＝－x²+6x－5，当a≤x≤a+3时，二次函数的最大值为y₁ ，最小值为y₂ ，若y₁－y₂＝3，求a的值．
答案解析收藏纠错 + 选题

三、拓展创新

19. (2024九上·金华开学考) 如图，已知在平面直角坐标系xOy中，一段抛物线. $\text{[math]}$ 记为抛物线C₁ ，它与x轴交于点O，A₁；将抛物线C₁绕点A₁旋转180°得抛物线C₂ ，交x轴于点A₁ ， A₂；将抛物线C₂绕点A₂ ，旋转180°得抛物线C₃ ，交x轴于点A₂ ， A₃；……如此进行下去，得到一条“波浪线”，若点M(2023，m)在此“波浪线”上，则m的值为（）

A . -9 B . -5 C . 9 D . 5

答案解析收藏纠错 + 选题
20. (2024九上·浙江期中) 在平面直角坐标系xOy中，我们称横坐标、纵坐标都为整数的点为“整点”．抛物线y＝ax²－2ax＋2a（a为常数）与直线y＝x交于M、N两点，若线段MN与抛物线围成的区域（含边界）内恰有4个“整点”，则a的取值范围是．

答案解析收藏纠错 + 选题
21. (2024九上·岱山开学考) 【定义】在平面直角坐标系中，对“纵横值”给出如下定义：点 $\text{[math]}$ 是函数图象上任意一点，纵坐标y与横坐标x的差“ $\text{[math]}$ ”称为点A的“纵横值”．函数图象上所有点的“纵横值”中的最大值称为函数的“最优纵横值”．
【举例】已知点 $\text{[math]}$ 在函数 $\text{[math]}$ 图象上．点 $\text{[math]}$ 的“纵横值”为 $\text{[math]}$ ；函数 $\text{[math]}$ 图象上所有点的“纵横值”可以表示为 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 的最大值为 $\text{[math]}$ ，所以函数 $\text{[math]}$ 的“最优纵横值”为7．
【问题】根据定义，解答下列问题：
1. （1） ①点 $\text{[math]}$ 的“纵横值”为；
  ②求出函数 $\text{[math]}$ 的“最优纵横值”；
2. （2）若二次函数 $\text{[math]}$ 的顶点在直线 $\text{[math]}$ 上，且最优纵横值为5，求c的值；
3. （3）若二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，二次函数的最优纵横值为2，直接写出b的值．
答案解析收藏纠错 + 选题