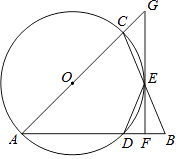
 B .
B .  C .
C .  D .
D . 

|
尺寸(cm) |
160 |
165 |
170 |
175 |
180 |
|
学生人数(人) |
1 |
3 |
2 |
2 |
2 |
则这10名学生校服尺寸的中位数为cm.
请根据图中提供的信息,解答下列问题:
设该种冰箱每台的销售价降低了x元.
每天售出的冰箱台数(台) | 每台冰箱的利润(元) | |
降价前 | 8 | |
降价后 |
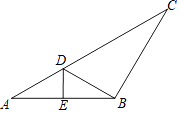
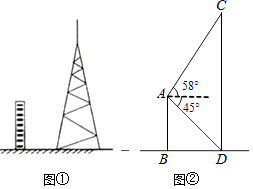
①求证:四边形BECD是菱形;
②当∠A为多少度时,四边形BECD是正方形?说明理由.
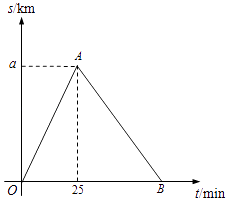
①求AB所在直线的函数表达式;
②该运动员跑完全程用时多少min?