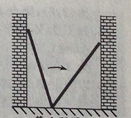
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为( )
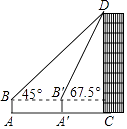
如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ≈1.414)( )
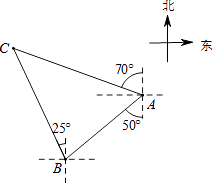
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
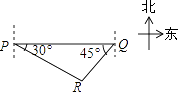 B .
B . 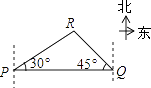 C .
C . 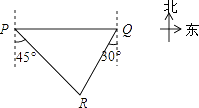 D .
D . 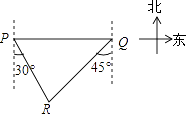
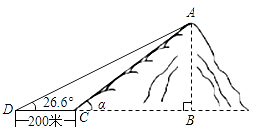
(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据: ≈1.41,
≈1.73)
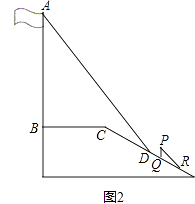
某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).