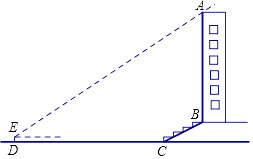
B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 



朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
① 填空:此次实验中,“1点朝上”的频率是;
② 小亮说:“根据实验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
请依据图中信息解答下列问题:

①“20元~25元”部分对应的圆心角度数为.
②捐款的中位数落在(填金额范围).
月份 | 用水量/立方米 | 水费/元 |
4 | 7 | 17 |
5 | 10 | 32 |
求该市居民用水的两种收费价格.