北京市海淀区2018届九年级上学期数学期末考试试卷

更新时间：2024-07-12 浏览次数：557 类型：期末考试

一、选择题

1. (2019九上·北京期中) 抛物线 $\text{[math]}$ 的对称轴是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·蜀山期末) 在△ABC中，∠C $\text{[math]}$ 90°．若AB $\text{[math]}$ 3，BC $\text{[math]}$ 1，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2018九上·海淀期末) 如图，线段BD，CE相交于点A，DE∥BC．若AB $\text{[math]}$ 4，AD $\text{[math]}$ 2，DE $\text{[math]}$ 1.5，则BC的长为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
4. (2021九上·福绵期中) 如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则 $\text{[math]}$ 的大小为（）

A . 30° B . 40° C . 50° D . 60°

答案解析收藏纠错 + 选题
5. (2018九上·海淀期末) 如图，△OAB∽△OCD，OA：OC $\text{[math]}$ 3：2，∠A $\text{[math]}$ α，∠C $\text{[math]}$ β，△OAB与△OCD的面积分别是 $\text{[math]}$ 和 $\text{[math]}$ ，△OAB与△OCD的周长分别是 $\text{[math]}$ 和 $\text{[math]}$ ，则下列等式一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·兰陵期中) 如图，在平面直角坐标系xOy中，点A从（3，4）出发，绕点O顺时针旋转一周，则点A不经过（）

A . 点M B . 点N C . 点P D . 点Q

答案解析收藏纠错 + 选题
7. (2018九上·海淀期末) 如图，反比例函数 $\text{[math]}$ 的图象经过点A（4，1），当 $\text{[math]}$ 时，x的取值范围是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·北京月考) 两个少年在绿茵场上游戏．小红从点A出发沿线段AB运动到点B，小兰从点C出发，以相同的速度沿⊙O逆时针运动一周回到点C，两人的运动路线如图1所示，其中AC $\text{[math]}$ DB．两人同时开始运动，直到都停止运动时游戏结束，其间他们与点C的距离y与时间x（单位：秒）的对应关系如图2所示．则下列说法正确的是（）

A . 小红的运动路程比小兰的长 B . 两人分别在1.09秒和7.49秒的时刻相遇 C . 当小红运动到点D的时候，小兰已经经过了点D D . 在4.84秒时，两人的距离正好等于⊙O的半径

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·大丰模拟) 方程 $\text{[math]}$ 的根为．

答案解析收藏纠错 + 选题
10. (2018九上·海淀期末) 已知∠A为锐角，且 $\text{[math]}$ ，那么∠A的大小是°．

答案解析收藏纠错 + 选题
11. (2023八下·东城期末) 若一个反比例函数图象的每一支上，y随x的增大而减小，则此反比例函数表达式可以是．（写出一个即可）

答案解析收藏纠错 + 选题
12. (2020九上·海淀期末) 如图，抛物线 $\text{[math]}$ 的对称轴为 $\text{[math]}$ ，点P，点Q是抛物线与x
轴的两个交点，若点P的坐标为（4，0），则点Q的坐标为．

答案解析收藏纠错 + 选题
13. (2020九上·伊通期末) 若一个扇形的圆心角为60°，面积为6π，则这个扇形的半径为．

答案解析收藏纠错 + 选题
14. (2018九上·海淀期末) 如图，AB是⊙O的直径，PA，PC分别与⊙O相切于点A，点C，若∠P $\text{[math]}$ 60°，PA $\text{[math]}$ $\text{[math]}$ ，则AB的长为．

答案解析收藏纠错 + 选题
15. (2018九上·杭州期末) 在同车道行驶的机动车，后车应当与前车保持足以采取紧急制动措施的安全距离．如图，在一个路口，一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处，小张驾驶一辆小轿车跟随大巴车行驶．设小张距大巴车尾x m，若大巴车车顶高于小张的水平视线0.8m，红灯下沿高于小张的水平视线3.2m，若小张能看到整个红灯，则x的最小值为．

答案解析收藏纠错 + 选题
16. (2018九上·海淀期末) 下面是“作一个30°角”的尺规作图过程．
已知：平面内一点A
求作： $\text{[math]}$ ，使得 $\text{[math]}$ =30°
做法：如图

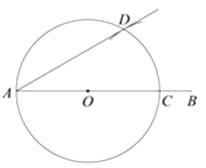
①作射线AB
②在射线AB上取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C
③以C为圆心，OC为半径作弧，与圆O交于点D，作射线AD，∠DAB即为所求的角
请回答：该尺规作图的依据是．

答案解析收藏纠错 + 选题

三、解答题

17. (2018九上·海淀期末) 计算： $\text{[math]}$ ° $\text{[math]}$ ° $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2018九上·海淀期末) 已知 $\text{[math]}$ 是关于x的方程 $\text{[math]}$ 的一个根，求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
19. (2018九上·海淀期末) 如图，在△ABC中，∠B为锐角， AB $\text{[math]}$ $\text{[math]}$ ，AC $\text{[math]}$ 5， $\text{[math]}$ ，求BC的长．

答案解析收藏纠错 + 选题
20. (2018九上·海淀期末) 码头工人每天往一艘轮船上装载30吨货物，装载完毕恰好用了8天时间．轮船到达目的地后开始卸货，记平均卸货速度为v（单位：吨/天），卸货天数为t．
1. （1）直接写出v关于t的函数表达式：v=；（不需写自变量的取值范围）
2. （2）如果船上的货物5天卸载完毕，那么平均每天要卸载多少吨？
答案解析收藏纠错 + 选题
21. (2019九上·福州期中) 如图，在△ABC中，∠B $\text{[math]}$ 90°，AB $\text{[math]}$ 4，BC $\text{[math]}$ 2，以AC为边作△ACE，∠ACE $\text{[math]}$ 90°，AC=CE，延长BC至点D，使CD $\text{[math]}$ 5，连接DE．求证：△ABC∽△CED．

答案解析收藏纠错 + 选题
22. (2018九上·海淀期末) 古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究：如图（图1中 $\text{[math]}$ 为锐角，图2中 $\text{[math]}$ 为直角，图3中 $\text{[math]}$ 为钝角）．
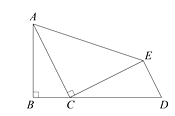
在△ABC的边BC上取 $\text{[math]}$ ， $\text{[math]}$ 两点，使 $\text{[math]}$ ，则 $\text{[math]}$ ∽ $\text{[math]}$ ∽ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，进而可得 $\text{[math]}$ $\text{[math]}$ （）（用 $\text{[math]}$ 表示）
若AB=4，AC=3，BC=6，则 $\text{[math]}$ $\text{[math]}$ （）．

答案解析收藏纠错 + 选题
23. (2018九上·海淀期末) 如图，函数 $\text{[math]}$ （ $\text{[math]}$ ）与 $\text{[math]}$ 的图象交于点A（-1，n）和点B（-2，1）．
1. （1）求k，a，b的值；
2. （2）直线 $\text{[math]}$ 与 $\text{[math]}$ （ $\text{[math]}$ ）的图象交于点P，与 $\text{[math]}$ 的图象交于点Q，当 $\text{[math]}$ 时，直接写出m的取值范围．
答案解析收藏纠错 + 选题
24. (2018九上·海淀期末) 如图，A，B，C三点在⊙O上，直径BD平分∠ABC，过点D作DE∥AB交弦BC于点E，在BC的延长线上取一点F，使得EF $\text{[math]}$ DE．
1. （1）求证：DF是⊙O的切线；
2. （2）连接AF交DE于点M，若 AD $\text{[math]}$ 4，DE $\text{[math]}$ 5，求DM的长．
答案解析收藏纠错 + 选题
25. (2018九上·海淀期末) 如图，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ °，点D是线段BC上的动点，将线段AD绕点A顺时针旋转50°至 $\text{[math]}$ ，连接 $\text{[math]}$ ．已知AB $\text{[math]}$ 2cm，设BD为x cm，B $\text{[math]}$ 为y cm．

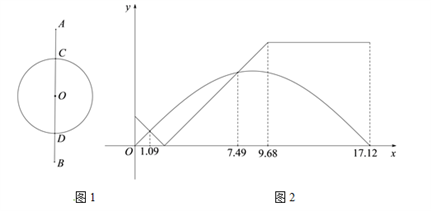
小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究，下面是小明的探究过程，请补充完整．（说明：解答中所填数值均保留一位小数）
1. （1）通过取点、画图、测量，得到了 $\text{[math]}$ 与 $\text{[math]}$ 的几组值，如下表：
  $\text{[math]}$
  $\text{[math]}$
  0.5
  0.7
  1.0
  1.5
  2.0
  2.3
  $\text{[math]}$
  1.7
  1.3
  1.1
  
  0.7
  0.9
  1.1
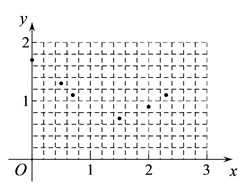
2. （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
3. （3）结合画出的函数图象，解决问题：
  线段 $\text{[math]}$ 的长度的最小值约为 $\text{[math]}$ ；
  若 $\text{[math]}$ $\text{[math]}$ ，则 $\text{[math]}$ 的长度x的取值范围是．
答案解析收藏纠错 + 选题
26. (2018九上·海淀期末) 已知二次函数 $\text{[math]}$ ．
1. （1）该二次函数图象的对称轴是x $\text{[math]}$ ；
2. （2）若该二次函数的图象开口向下，当 $\text{[math]}$ 时， $\text{[math]}$ 的最大值是2，求当 $\text{[math]}$ 时， $\text{[math]}$ 的最小值；
3. （3）若对于该抛物线上的两点 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ 时，均满足 $\text{[math]}$ ，请结合图象，直接写出 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
27. (2018九上·海淀期末) 对于⊙C与⊙C上的一点A，若平面内的点P满足：射线AP与⊙C交于点Q（点Q可以与点P重合），且 $\text{[math]}$ ，则点P称为点A关于⊙C的“生长点”．
已知点O为坐标原点，⊙O的半径为1，点A（-1，0）．
1. （1）若点P是点A关于⊙O的“生长点”，且点P在x轴上，请写出一个符合条件的点P的坐标；
2. （2）若点B是点A关于⊙O的“生长点”，且满足 $\text{[math]}$ ，求点B的纵坐标t的取值范围；
3. （3）直线 $\text{[math]}$ 与x轴交于点M，与y轴交于点N，若线段MN上存在点A关于⊙O的“生长点”，直接写出b的取值范围是．
答案解析收藏纠错 + 选题
28. (2018九上·海淀期末) 在△ABC中，∠A $\text{[math]}$ 90°，AB $\text{[math]}$ AC．
1. （1）如图1，△ABC的角平分线BD，CE交于点Q，请判断“ $\text{[math]}$ ”是否正确：（填“是”或“否”）；
2. （2）点P是△ABC所在平面内的一点，连接PA，PB，且PB $\text{[math]}$ $\text{[math]}$ PA．
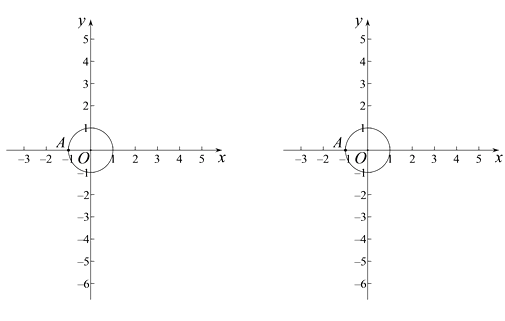
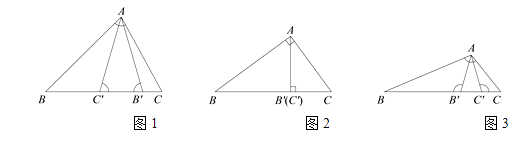
  ①如图2，点P在△ABC内，∠ABP $\text{[math]}$ 30°，求∠PAB的大小；
  ②如图3，点P在△ABC外，连接PC，设∠APC $\text{[math]}$ α，∠BPC $\text{[math]}$ β，用等式表示α，β之间的数量关系，并证明你的结论．
答案解析收藏纠错 + 选题