①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
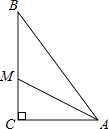

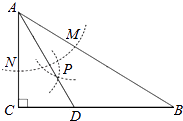
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.







①作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;
②作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.

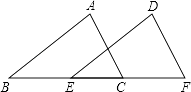
已知:如图,AD是△ABC的角平分线,点E在BC上,点F在CA的延长线上,EF∥AD,EF交AB于点G.
求证:∠3=∠F
证明:因为AD是△ABC的角平分线 ( 已知 )
所以∠1=∠2 ( )
因为EF∥AD(已知)
所以∠3=∠ ()
∠F=∠ ( )
所以∠3=∠F( ).





①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?