| 50 | 52 | 54 | 56 | 58 | |
| 1 | 2 | 3 | 4 | 5 |
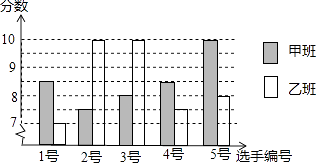
参考数据:
|
|
平均数 |
中位数 |
众数 |
方差 |
|
甲班 |
|
|
|
|
|
乙班 |
|
|
10 |
|
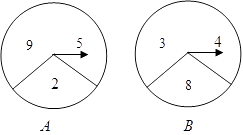
销售单价 | x |
销售量 | |
销售玩具获得利润 |
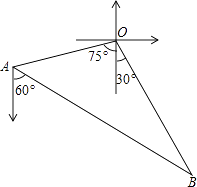
以点为圆心,以线段的长为半径画弧,与射线BA交于点D,使线段OD的长等于
连OD,在OD上画出点P,使OP的长等于
,请写出画法,并说明理由.
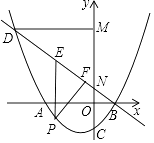
如图1,点A为线段BC外一动点,且 ,填空:当点A位于时,线段AC的长取得最大值,且最大值为
用含
的式子表示
.
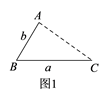
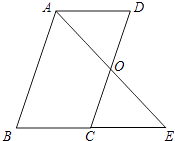
点A为线段BC外一动点,且 ,如图2所示,分别以
为边,作等边三角形ABD和等边三角形ACE,连接
,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
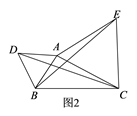
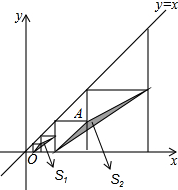
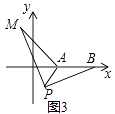
①如图3,在平面直角坐标系中,点A的坐标为 ,点B的坐标为
,点P为线段AB外一动点,且
,求线段AM长的最大值及此时点P的坐标.
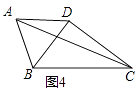
如图4,在四边形ABCD中,
,若对角线
于点D,请直接写出对角线AC的最大值.