山东省聊城市2018年中考数学试卷

更新时间：2018-08-10 浏览次数：751 类型：中考真卷

一、选择题

1. (2018·聊城) 下列实数中的无理数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·河北模拟) 如图所示的几何体，它的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九下·长沙月考) 在运算速度上，已连续多次取得世界第一的神威太湖之光超级计算机，其峰值性能为12.5亿亿次/秒．这个数据以亿次/秒为单位用科学记数法可以表示为（）

A . 1.25×10⁸亿次/秒 B . 1.25×10⁹亿次/秒 C . 1.25×10¹⁰亿次/秒 D . 12.5×10⁸亿次/秒

答案解析收藏纠错 + 选题
4. (2022·滨城模拟) 如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD=95°，∠CDE=25°，则∠DEF的度数是（）

A . 110° B . 115° C . 120° D . 125°

答案解析收藏纠错 + 选题
5. (2020七下·咸阳月考) 下列计算错误的是（）

A . a²÷a⁰•a²=a⁴ B . a²÷（a⁰•a²）=1 C . （﹣1.5）⁸÷（﹣1.5）⁷=﹣1.5 D . ﹣1.5⁸÷（﹣1.5）⁷=﹣1.5

答案解析收藏纠错 + 选题
6. (2018·聊城) 已知不等式 $\text{[math]}$ ，其解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2020九上·宁都期末) 如图，⊙O中，弦BC与半径OA相交于点D，连接AB，OC．若∠A=60°，∠ADC=85°，则∠C的度数是（）

A . 25° B . 27.5° C . 30° D . 35°

答案解析收藏纠错 + 选题
8. (2022八上·龙口开学考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九上·昆都仑期末) 小亮、小莹、大刚三位同学随机地站成一排合影留念，小亮恰好站在中间的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019八上·重庆月考) 如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A=α，∠CEA′=β，∠BDA'=γ，那么下列式子中正确的是（）

A . γ=2α+β B . γ=α+2β C . γ=α+β D . γ=180°﹣α﹣β

答案解析收藏纠错 + 选题
11. (2021·淄川模拟) 如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴和y轴上，并且OA=5，OC=3．若把矩形OABC绕着点O逆时针旋转，使点A恰好落在BC边上的A₁处，则点C的对应点C₁的坐标为（）

A . （﹣ $\text{[math]}$ ） B . （﹣ $\text{[math]}$ ） C . （﹣ $\text{[math]}$ ） D . （﹣ $\text{[math]}$ ）

答案解析收藏纠错 + 选题
12. (2020九上·临清期末) 春季是传染病多发的季节，积极预防传染病是学校高度重视的一项工作，为此，某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中，先经过 $\text{[math]}$ 的集中药物喷洒，再封闭宿舍 $\text{[math]}$ ，然后打开门窗进行通风，室内每立方米空气中含药量 $\text{[math]}$ 与药物在空气中的持续时间 $\text{[math]}$ 之间的函数关系，在打开门窗通风前分别满足两个一次函数，在通风后又成反比例，如图所示.下面四个选项中错误的是（）

A . 经过 $\text{[math]}$ 集中喷洒药物，室内空气中的含药量最高达到 $\text{[math]}$ B . 室内空气中的含药量不低于 $\text{[math]}$ 的持续时间达到了 $\text{[math]}$ C . 当室内空气中的含药量不低于 $\text{[math]}$ 且持续时间不低于35分钟，才能有效杀灭某种传染病毒.此次消毒完全有效 D . 当室内空气中的含药量低于 $\text{[math]}$ 时，对人体才是安全的，所以从室内空气中的含药量达到 $\text{[math]}$ 开始，需经过 $\text{[math]}$ 后，学生才能进入室内

答案解析收藏纠错 + 选题

二、填空题

13. (2019·扬州模拟) 已知关于x的方程（k﹣1）x²﹣2kx+k﹣3=0有两个相等的实根，则k的值是．

答案解析收藏纠错 + 选题
14. (2021七下·临淄期中) 某十字路口设有交通信号灯，东西向信号灯的开启规律如下：红灯开启30秒后关闭，紧接着黄灯开启3秒后关闭，再紧接着绿灯开启42秒，按此规律循环下去.如果不考虑其他因素，当一辆汽车沿东西方向随机地行驶到该路口时，遇到红灯的概率是．

答案解析收藏纠错 + 选题
15. (2018·聊城) 用一块圆心角为216°的扇形铁皮，做一个高为40cm的圆锥形工件（接缝忽略不计），那么这个扇形铁皮的半径是cm．

答案解析收藏纠错 + 选题
16. (2024八上·西塘开学考) 如果一个正方形被截掉一个角后，得到一个多边形，那么这个多边形的内角和是．

答案解析收藏纠错 + 选题
17. (2023七下·渝中期中) 若 $\text{[math]}$ 为实数，则 $\text{[math]}$ 表示不大于 $\text{[math]}$ 的最大整数，例如 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 等. $\text{[math]}$ 是大于 $\text{[math]}$ 的最小整数，对任意的实数 $\text{[math]}$ 都满足不等式 $\text{[math]}$ . ①，利用这个不等式①，求出满足 $\text{[math]}$ 的所有解，其所有解为．

答案解析收藏纠错 + 选题

三、解答题

18. (2019·新余模拟) 先化简，再求值：
$\text{[math]}$ ，其中 $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2020·大连模拟) 时代中学从学生兴趣出发，实施体育活动课走班制.为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1200名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：
球类名称
乒乓球
羽毛球
排球
篮球
足球
人数
42
$\text{[math]}$
15
33
$\text{[math]}$

解答下列问题：
1. （1）这次抽样调查中的样本是；
2. （2）统计表中， $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）试估计上述1200名学生中最喜欢乒乓球运动的人数.
答案解析收藏纠错 + 选题
20. (2022八下·孟村期中) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ ，过 $\text{[math]}$ 点作 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ .
2. （2）若正方形边长是5， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
21. (2018·聊城) 建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方，原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要，公司抽调甲队外援施工，由乙队先单独施工40天后甲队返回，两队又共同施工了110天，这时甲乙两队共完成土方量103.2万立方.
1. （1）问甲、乙两队原计划平均每天的施工土方量分别为多少万立方？
2. （2）在抽调甲队外援施工的情况下，为了保证150天完成任务，公司为乙队新购进了一批机械来提高效率，那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务？
答案解析收藏纠错 + 选题
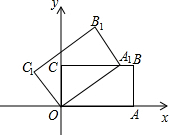
22. (2018·聊城) 随着我市农产品整体品牌形象“聊•胜一筹!”的推出，现代农业得到了更快发展．某农场为扩大生产建设了一批新型钢管装配式大棚，如图1．线段AB，BD分别表示大棚的墙高和跨度，AC表示保温板的长．已知墙高AB为2米，墙面与保温板所成的角∠BAC=150°，在点D处测得A点、C点的仰角分别为9°，15.6°，如图2．求保温板AC的长是多少米？（精确到0.1米）
（参考数据： $\text{[math]}$ ≈0.86，sin9°≈0.16，cos9°≈0.99，tan9°≈0.16，sin15.6°≈0.27，cos15.6°≈0.96，tan15.6°≈0.28）

答案解析收藏纠错 + 选题
23. (2018·聊城) 如图，已知反比例函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象关于 $\text{[math]}$ 轴对称， $\text{[math]}$ ， $\text{[math]}$ 是函数 $\text{[math]}$ 图象上的两点，连接 $\text{[math]}$ ，点 $\text{[math]}$ 是函数 $\text{[math]}$ 图象上的一点，连接 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值；
2. （2）求 $\text{[math]}$ 所在直线的表达式；
3. （3）求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
24. (2022·滨城模拟) 如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆．
1. （1）求证：AC是⊙O的切线；
2. （2）已知⊙O的半径为2.5，BE=4，求BC，AD的长．
答案解析收藏纠错 + 选题
25. (2018·聊城) 如图，已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于原点 $\text{[math]}$ 和点 $\text{[math]}$ ，与对称轴 $\text{[math]}$ 交于点 $\text{[math]}$ .矩形 $\text{[math]}$ 的边 $\text{[math]}$ 在 $\text{[math]}$ 轴正半轴上，且 $\text{[math]}$ ，边 $\text{[math]}$ ， $\text{[math]}$ 与抛物线分别交于点 $\text{[math]}$ ， $\text{[math]}$ .当矩形 $\text{[math]}$ 沿 $\text{[math]}$ 轴正方向平移，点 $\text{[math]}$ ， $\text{[math]}$ 位于对称轴 $\text{[math]}$ 的同侧时，连接 $\text{[math]}$ ，此时，四边形 $\text{[math]}$ 的面积记为 $\text{[math]}$ ；点 $\text{[math]}$ ， $\text{[math]}$ 位于对称轴 $\text{[math]}$ 的两侧时，连接 $\text{[math]}$ ， $\text{[math]}$ ，此时五边形 $\text{[math]}$ 的面积记为 $\text{[math]}$ .将点 $\text{[math]}$ 与点 $\text{[math]}$ 重合的位置作为矩形 $\text{[math]}$ 平移的起点，设矩形 $\text{[math]}$ 平移的长度为 $\text{[math]}$ .
1. （1）求出这条抛物线的表达式；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
3. （3）当矩形 $\text{[math]}$ 沿着 $\text{[math]}$ 轴的正方向平移时，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式，并求出 $\text{[math]}$ 为何值时， $\text{[math]}$ 有最大值，最大值是多少？
答案解析收藏纠错 + 选题