人教版九年级数学上册期末检测卷

更新时间：2018-12-13 浏览次数：1062 类型：期末考试

一、选择题

1. (2017·西固模拟) 若反比例函数y=﹣ $\text{[math]}$ 的图象经过点A（3，m），则m的值是（）

A . ﹣3 B . 3 C . ﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2016·葫芦岛) 下列图形既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 下列事件中，必然发生的是（）

A . 某射击运动射击一次，命中靶心 B . 通常情况下，水加热到100℃时沸腾 C . 掷一次骰子，向上的一面是6点 D . 抛一枚硬币，落地后正面朝上

答案解析收藏纠错 + 选题
4. (2017·兰山模拟) 如图，直线y=kx与双曲线y=﹣ $\text{[math]}$ 交于A（x₁ ， y₁），B（x₂ ， y₂）两点，则2x₁y₂﹣8x₂y₁的值为（）

A . ﹣6 B . ﹣12 C . 6 D . 12

答案解析收藏纠错 + 选题
5. (2016九上·仙游期末) 如上图，经过原点O的⊙P与 $\text{[math]}$ 、 $\text{[math]}$ 轴分别交于A、B两点，点C是劣弧 $\text{[math]}$ 上一点，则∠ACB=（）

A . 80° B . 90° C . 100° D . 无法确定

答案解析收藏纠错 + 选题
6. (2018九上·潮南期末)
在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（　　）

A . 40cm B . 60cm C . 80cm D . 100cm

答案解析收藏纠错 + 选题
7. (2017·泰兴模拟) 如图，在平面直角坐标系中，点B，C，E，在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（）

A . △ABC绕点C顺时针旋转90°，再向下平移3 B . △ABC绕点C顺时针旋转90°，再向下平移1 C . △ABC绕点C逆时针旋转90°，再向下平移1 D . △ABC绕点C逆时针旋转90°，再向下平移3

答案解析收藏纠错 + 选题
8. (2019九上·黄石期中) 抛物线y=（m﹣1）x²﹣mx﹣m²+1的图象过原点，则m的值为（　　）

A . ±1 B . 0 C . 1 D . -1

答案解析收藏纠错 + 选题
9. 圆的面积公式S=πR²中，S与R之间的关系是（）

A . S是R的正比例函数 B . S是R的一次函数 C . S是R的二次函数 D . 以上答案都不对

答案解析收藏纠错 + 选题
10.
如图，P是⊙O直径AB延长线上的一点，PC与⊙O相切于点C，若∠P=20°，则∠A的度数为（　　）

A . 40° B . 35° C . 30° D . 25°

答案解析收藏纠错 + 选题
11.
如图，一个大正方形中有2个小正方形，如果它们的面积分别是S₁ ， S₂ ，则（　　)

A . S₂＞S₁ B . S₁=S₂ C . S₁＞S₂ D . S₁≥S₂

答案解析收藏纠错 + 选题
12. (2017·阿坝) 如图，抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
①4ac＜b²；
②方程ax²+bx+c=0的两个根是x₁=﹣1，x₂=3；
③3a+c＞0
④当y＞0时，x的取值范围是﹣1≤x＜3
⑤当x＜0时，y随x增大而增大
其中结论正确的个数是（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题

13. (2018九上·邗江期中) 把方程3x（x﹣2）=4（x+1）化为一元二次方程的一般形式是；

答案解析收藏纠错 + 选题
14.
小球在如图所示的地板上自由滚动，并随机地停留在某块方砖上，每一块方砖除颜色外完全相同，它最终停留在黑色方砖上的概率是 .

答案解析收藏纠错 + 选题
15. (2016·齐齐哈尔) 一个侧面积为16 $\text{[math]}$ πcm²的圆锥，其主视图为等腰直角三角形，则这个圆锥的高为cm．

答案解析收藏纠错 + 选题
16. (2018九上·长春开学考) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有实数解，那么实数 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
17.
如图，以点O为位似中心，将△ABC放大得到△DEF，若AD=OA，则△ABC与△DEF的面积之比为．

答案解析收藏纠错 + 选题
18. (2017·宜兴模拟) 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是．

答案解析收藏纠错 + 选题

三、解答题（一）

19. (2017·兰州模拟) 解方程：x²+3x﹣2=0．

答案解析收藏纠错 + 选题
20. (2018九上·青海期中) 如图为桥洞的形状，其正视图是由 $\text{[math]}$ 和矩形ABCD构成．O点为 $\text{[math]}$ 所在⊙O的圆心，点O又恰好在AB为水面处．若桥洞跨度CD为8米，拱高（OE⊥弦CD于点F ）EF为2米．求 $\text{[math]}$ 所在⊙O的半径DO．

答案解析收藏纠错 + 选题
21.
如图所示的网格图中，每小格都是边长为1的正方形，△ABC的三个顶点都在格点上，在建立直角坐标系后，点C的坐标（-1，2）

（1）画出△ABC绕点D（0，5）逆时针旋转90°后的△A₁B₁C₁ ，
（2）写出A₁ ， C₁的坐标.
（3）求点A旋转到A₁所经过的路线长.

答案解析收藏纠错 + 选题
22. (2017九上·东丽期末) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，作直线 $\text{[math]}$ ．动点 $\text{[math]}$ 在 $\text{[math]}$ 轴上运动，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，交抛物线于点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．
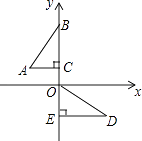
（Ⅰ）求抛物线的解析式和直线 $\text{[math]}$ 的解析式；
（Ⅱ）当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上运动时，求线段 $\text{[math]}$ 的最大值；
（Ⅲ）当以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形是平行四边形时，直接写出 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题

四、解答题（二）

23. (2017·蒙自模拟) 有红、黄两个盒子，红盒子中装有编号分别为1、2、3、4的四个红球，黄盒子中装有编号为1、2、3的三个黄球．甲、乙两人玩摸球游戏，游戏规则为：甲从红盒子中每次摸出一个小球，乙从黄盒子中每次摸出一个小球，若两球编号之和为奇数，则甲胜，否则乙胜．
1. （1）试用列表或画树形图的方法，求甲获胜的概率；
2. （2）请问这个游戏规则对甲、乙双方公平吗？请说明理由．
答案解析收藏纠错 + 选题
24. (2017·武汉模拟) 如图，在平面直角坐标系xOy中，双曲线y= $\text{[math]}$ 与直线y=﹣2x+2交于点A（﹣1，a）．
1. （1）求a，m的值；
2. （2）求该双曲线与直线y=﹣2x+2另一个交点B的坐标．
答案解析收藏纠错 + 选题
25. (2016·成都)
如图，在Rt△ABC中，∠ABC=90°，以CB为半径作⊙C，交AC于点D，交AC的延长线于点E，连接ED，BE．
1. （1）求证：△ABD∽△AEB；
2. （2）当 $\text{[math]}$ = $\text{[math]}$ 时，求tanE；
3. （3）在（2）的条件下，作∠BAC的平分线，与BE交于点F，若AF=2，求⊙C的半径．
答案解析收藏纠错 + 选题
26. (2017·潍坊模拟) 如图1，若△ABC和△ADE为等边三角形，M，N分别为EB，CD的中点，易证：CD=BE，△AMN是等边三角形：
1. （1）当把△ADE绕点A旋转到图2的位置时，CD=BE吗？若相等请证明，若不等于请说明理由；
2. （2）当把△ADE绕点A旋转到图3的位置时，△AMN还是等边三角形吗？若是请证明，若不是，请说明理由（可用第一问结论）．
答案解析收藏纠错 + 选题
27. (2019九上·深圳期中)
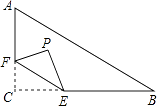
已知，如图①，在▱ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM停止平移时，点Q也停止移动，如图②，设移动时间为t（s）（0＜t＜4），连接PQ，MQ，MC，解答下列问题：
1. （1）当t为何值时，PQ∥MN？
2. （2）设△QMC的面积为y（cm²），求y与t之间的函数关系式；
3. （3）是否存在某一时刻t，使S_△QMC：S_{四边形ABQP}=1：4？若存在，求出t的值；若不存在，请说明理由．
4. （4）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题