浙江省舟山普陀区2018届数学中考模拟试卷

更新时间：2019-04-03 浏览次数：421 类型：中考模拟

一、单选题

1. (2018·普陀模拟) 2018 的相反数是（）

A . -2018 B . - C . 2018 D .

答案解析收藏纠错 + 选题
2. (2021·安阳模拟) 已知一个几何体的三种视图如图所示，则该几何体是（）

A . 三棱柱 B . 三棱锥 C . 圆锥 D . 圆柱

答案解析收藏纠错 + 选题
3. (2018·普陀模拟) 下列计算，正确的是（）

A . a²﹣a=a B . a²•a³=a⁶ C . a⁹÷a³=a³ D . （a³）²=a⁶

答案解析收藏纠错 + 选题
4. (2018·普陀模拟) 在△ABC中，AB=5，AC=8，则BC长不可能是（）

A . 4 B . 8 C . 10 D . 13

答案解析收藏纠错 + 选题
5. (2021八下·嵊州期末) 一元二次方程x²－8x＝48可表示成(x－a)²＝48＋b的形式，其中a，b为整数，求a＋b之值为何（）

A . 20 B . 12 C . －12 D . －20

答案解析收藏纠错 + 选题
6. (2018·普陀模拟) 若x+5＞0，则（）

A . x+1＜0 B . x﹣1＜0 C . ＜﹣1 D . ﹣2x＜12

答案解析收藏纠错 + 选题
7. (2019七下·文登期末) 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．
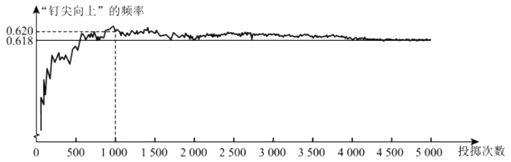
下面有三个推断：
①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；
②随着试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
③若再次用计算机模拟此实验，则当投掷次数为1000时，“钉尖向上”的频率一定是0.620．
其中合理的是（）

A . ① B . ② C . ①② D . ①③

答案解析收藏纠错 + 选题
8. (2018·普陀模拟) 如图，在矩形ABCD中，AB=5，BC=7，点E是AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A₁恰好落在∠BCD的平分线上时，则AE的长为（）

A . 2或3 B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . 3或4

答案解析收藏纠错 + 选题
9. (2018·普陀模拟) 给出下列四个命题：
（ 1 ）若点A在直线y=2x-3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限；（2）若A（a，m）、B（a-1，n）（a＞0）在反比例函数y= $\text{[math]}$

的图象上，则m＜n；（3）一次函数y=-2x-3的图象不经过第三象限；（4）二次函数y=-2x²-8x+1的最大值是9.

正确命题的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

10. (2019·平阳模拟) 分解因式：x²﹣9=．

答案解析收藏纠错 + 选题
11. (2022七下·荷塘期末) 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：

甲
乙
丙
丁
平均数
9.14
9.15
9.14
9.15
方差
6.6
6.8
6.7
6.6
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择．

答案解析收藏纠错 + 选题
12. (2018·普陀模拟) 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB =.

答案解析收藏纠错 + 选题
13. (2019·陕西模拟) 写出一个比3大且比4小的无理数：.

答案解析收藏纠错 + 选题
14. (2018·普陀模拟) 如图是圆心角为 30°，半径分别是 1、3、5、7、…的扇形组成的图形，阴影部分的面积依次记为 S1、S2、S3、…，则 S3=，Sn=.结果保留 π）

答案解析收藏纠错 + 选题
15. (2018·普陀模拟) 如图，一个边长为2 的正六边形的边CD 在x 轴上，正六边形的中心M 在y 轴上，现在把这个正六边形沿x 轴无滑动的滚动一周，则顶点A 的坐标为(， )，若滚动100 周，中心M 经过的路径长.

答案解析收藏纠错 + 选题

三、解答题

16. (2018·普陀模拟)
1. （1）计算： (1 - $\text{[math]}$ )0 - + $\text{[math]}$
2. （2）化简： (a - b) 2 - a(a - 2b)
答案解析收藏纠错 + 选题
17. (2018·普陀模拟) 解方程： $\text{[math]}$ =1．

答案解析收藏纠错 + 选题
18. (2020八上·嵩县期末) 如图，已知：AB∥CD．
1. （1）在图中，用尺规作∠ACD 的平分线交 AB 于 E 点；
2. （2）判断△ACE 的形状，并证明.
答案解析收藏纠错 + 选题

19. (2018·普陀模拟) 某工厂甲、乙两个部门各有员工 400 人，为了解这两个部门员工的生产技能情况，从甲、乙两个部门各随机抽取 20 名员工，进行了生产技能测试，测试成绩（百分制），通过数据的收集、整理、分析得到下表：

成绩 x	甲	乙
40≤x≤49	0	1
50≤x ≤59	0	0
60≤x≤69	1	0
70 ≤x≤79	11	7
80 ≤x ≤89	7	10
90 ≤ x ≤ 100	1	2

部门	平均数	中位数	众数
甲	78.3	77.5	75
乙	78	80.5	81

（说明：成绩 80 分及以上为生产技能优秀，70--79 分为生产技能良好，60--69 分为生产技能合格，60 分以下为生产技能不合格）得出结论：

（1）估计乙部门生产技能优秀的员工人数为；
（2）可以推断出部门员工的生产技能水平较高，理由为.（至少从两个不同的角度说明推断的合理性）

答案解析收藏纠错 + 选题

20. (2020九上·郑州月考)
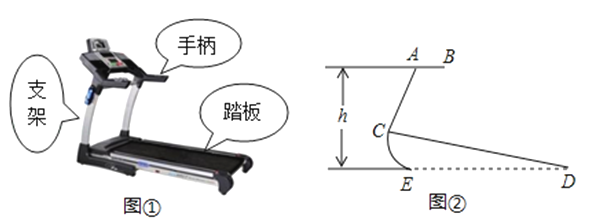
图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1.6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0.8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0.1m）．
（参考数据：sin12°=cos78°≈0.21，sin68°=cos22°≈0.93，tan68°≈2.48）

答案解析收藏纠错 + 选题
21. (2018·普陀模拟) 经过实验获得两个变量 x(x > 0)， y( y > 0) 的一组对应值如下表。

x

1

2

3

4

5

6

7

y

7

3.5

2.33

1.75

1.4

1.17

1
1. （1）在网格中建立平面直角坐标系，画出相应的函数图象，求出这个函数表达式；
2. （2）结合函数图象解决问题：（结果保留一位小数）
  ① $\text{[math]}$ 的值约为多少？
  
  ②点A坐标为（6，0），点B在函数图象上，OA=OB，则点B的横坐标约是多少？
答案解析收藏纠错 + 选题
22. (2018·普陀模拟) 在 Rt△ABC 中，∠C=90°，AC=2BC，AB=5，D、E 分别在 AB、AC 上，且 AE = $\text{[math]}$ ，DE∥BC．
1. （1）如图（1），将△ADE 沿射线 DA 方向平移，得到△ A1 D1 E1 ，当 AD1 多大时，四边形 AA1 E1 E 为菱形；
2. （2）如图（2），将△ADE 绕 A 点顺时针旋转a 度（ 00 < a < 1800 ）得到△AD₂E₂
  ①连结 CE2 ， BD2 ，求： $\text{[math]}$ 的值；
  
  ②连结 CE2 ， BE2 若△ ACE2 是直角三角形，求：△ ABE 2 的面积.
答案解析收藏纠错 + 选题