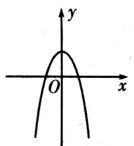
 B .
B . 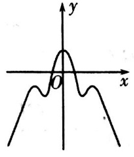 C .
C . 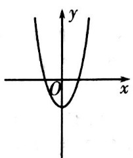 D .
D . 
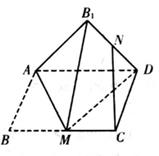
①存在某个位置,使得 ;②翻折过程中,
的长是定值;③若
,则
;④若
,当三棱锥
的体积最大时,三棱锥
的外接球的表面积是
.
| | 0 | 1 | 2 | 3 | 4 |
| | 15 | 12 | 11 | 9 | 8 |
附:回归方程 中斜率和截距的最小二乘法估计公式分别为:
,
.