2013年四川省资阳市中考数学试卷

更新时间：2024-07-12 浏览次数：1370 类型：中考真卷

一、选择题

1. (2013·资阳) 16的平方根是（）

A . 4 B . ±4 C . 8 D . ±8

答案解析收藏纠错 + 选题
2. (2020·宜兴模拟) 一个正多边形的每个外角都等于36°，那么它是（）

A . 正六边形 B . 正八边形 C . 正十边形 D . 正十二边形

答案解析收藏纠错 + 选题
3. (2013·资阳) 在一个不透明的盒子里，装有4个黑球和若干个白球，它们除颜色外没有任何其他区别，摇匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复，共摸球40次，其中10次摸到黑球，则估计盒子中大约有白球（）

A . 12个 B . 16个 C . 20个 D . 30个

答案解析收藏纠错 + 选题
4. (2021八下·老河口期末) 在函数y= $\text{[math]}$ 中，自变量x的取值范围是（）

A . x≤1 B . x≥1 C . x＜1 D . x＞1

答案解析收藏纠错 + 选题
5. (2013·资阳) 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（）

A . 48 B . 60 C . 76 D . 80

答案解析收藏纠错 + 选题
6. (2013·资阳) 资阳市2012年财政收入取得重大突破，地方公共财政收入用四舍五入取近似值后为27.39亿元，那么这个数值（）

A . 精确到亿位 B . 精确到百分位 C . 精确到千万位 D . 精确到百万位

答案解析收藏纠错 + 选题
7. (2013·资阳) 钟面上的分针的长为1，从9点到9点30分，分针在钟面上扫过的面积是（）

A . $\text{[math]}$ π B . $\text{[math]}$ π C . $\text{[math]}$ π D . π

答案解析收藏纠错 + 选题
8. (2013·资阳) 在芦山地震抢险时，太平镇部分村庄需8组战士步行运送物资，要求每组分配的人数相同，若按每组人数比预定人数多分配1人，则总数会超过100人；若按每组人数比预定人数少分配1人，则总数不够90人，那么预定每组分配的人数是（）

A . 10人 B . 11人 C . 12人 D . 13人

答案解析收藏纠错 + 选题
9. (2013·资阳)
从所给出的四个选项中，选出适当的一个填入问号所在位置，使之呈现相同的特征（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2022·临安模拟) 如图，抛物线y=ax²+bx+c（a≠0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a﹣b+c，则P的取值范围是（）

A . ﹣4＜P＜0 B . ﹣4＜P＜﹣2 C . ﹣2＜P＜0 D . ﹣1＜P＜0

答案解析收藏纠错 + 选题

二、填空题

11. (2013·资阳) （﹣a²b）²•a=．

答案解析收藏纠错 + 选题
12. (2013·资阳) 若一组2，﹣1，0，2，﹣1，a的众数为2，则这组数据的平均数为．

答案解析收藏纠错 + 选题
13. (2013·资阳) 在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=60°，AC=10，则AB=．

答案解析收藏纠错 + 选题
14. (2013·资阳) 2013•资阳）在一次函数y=（2﹣k）x+1中，y随x的增大而增大，则k的取值范围为．

答案解析收藏纠错 + 选题
15. (2023八下·佛冈期中) 如图，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是．

答案解析收藏纠错 + 选题
16. (2013·资阳) 已知直线上有n（n≥2的正整数）个点，每相邻两点间距离为1，从左边第1个点起跳，且同时满足以下三个条件：
①每次跳跃均尽可能最大；
②跳n次后必须回到第1个点；
③这n次跳跃将每个点全部到达，
设跳过的所有路程之和为S_n ，则S₂₅=．

答案解析收藏纠错 + 选题

三、解答题

17. (2022八上·临武期中) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2013·资阳) 体考在即，初三（1）班的课题研究小组对本年级530名学生的体育达标情况进行调查，制作出如图所示的统计图，其中1班有50人．（注：30分以上为达标，满分50分）根据统计图，解答下面问题：
1. （1）初三（1）班学生体育达标率和本年级其余各班学生体育达标率各是多少？
2. （2）若除初三（1）班外其余班级学生体育考试成绩在30﹣﹣40分的有120人，请补全扇形统计图；（注：请在图中分数段所对应的圆心角的度数）
3. （3）如果要求全年级学生的体育达标率不低于90%，试问在本次调查中，该年级全体学生的体育达标率是否符合要求？
答案解析收藏纠错 + 选题
19. (2013·资阳) 在关于x，y的二元一次方程组 $\text{[math]}$ 中．
1. （1）若a=3．求方程组的解；
2. （2）若S=a（3x+y），当a为何值时，S有最值．
答案解析收藏纠错 + 选题
20. (2013·资阳) 在⊙O中，AB为直径，点C为圆上一点，将劣弧 $\text{[math]}$ 沿弦AC翻折交AB于点D，连结CD．
1. （1）如图1，若点D与圆心O重合，AC=2，求⊙O的半径r；
2. （2）如图2，若点D与圆心O不重合，∠BAC=25°，请直接写出∠DCA的度数．
答案解析收藏纠错 + 选题
21. (2020九上·桐城期末)
如图，已知直线l分别与x轴、y轴交于A，B两点，与双曲线y= $\text{[math]}$ （a≠0，x＞0）分别交于D、E两点．
1. （1）若点D的坐标为（4，1），点E的坐标为（1，4）：
  ①分别求出直线l与双曲线的解析式；
  ②若将直线l向下平移m（m＞0）个单位，当m为何值时，直线l与双曲线有且只有一个交点？
2. （2）假设点A的坐标为（a，0），点B的坐标为（0，b），点D为线段AB的n等分点，请直接写出b的值．
答案解析收藏纠错 + 选题
22. (2013·资阳)
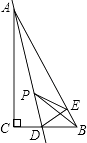
钓鱼岛历来是中国领土，以它为圆心在周围12海里范围内均属于禁区，不允许它国船只进入，如图，今有一中国海监船在位于钓鱼岛A正南方距岛60海里的B处海域巡逻，值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船，正以9节的速度沿正东方向驶向钓鱼岛，中方立即向日本渔船发出警告，并沿北偏西30°的方向以12节的速度前往拦截，期间多次发出警告，2小时候海监船到达D处，与此同时日本渔船到达E处，此时海监船再次发出严重警告．
1. （1）当日本渔船受到严重警告信号后，必须沿北偏东转向多少度航行，才能恰好避免进入钓鱼岛12海里禁区？
2. （2）当日本渔船不听严重警告信号，仍按原速度，原方向继续前进，那么海监船必须尽快到达距岛12海里，且位于线段AC上的F处强制拦截渔船，问海监船能否比日本渔船先到达F处？（注：①中国海监船的最大航速为18节，1节=1海里/小时；②参考数据：sin26.3°≈0.44，sin20.5°≈0.35，sin18.1°≈0.31， $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7）
答案解析收藏纠错 + 选题
23. (2013·资阳)
在一个边长为a（单位：cm）的正方形ABCD中，点E、M分别是线段AC，CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．
1. （1）如图1，当点M与点C重合，求证：DF=MN；
2. （2）如图2，假设点M从点C出发，以1cm/s的速度沿CD向点D运动，点E同时从点A出发，以 $\text{[math]}$ cm/s速度沿AC向点C运动，运动时间为t（t＞0）；
  ①判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由．
  ②连结FM、FN，△MNF能否为等腰三角形？若能，请写出a，t之间的关系；若不能，请说明理由．
答案解析收藏纠错 + 选题
24. (2013·资阳)
如图，四边形ABCD是平行四边形，过点A、C、D作抛物线y=ax²+bx+c（a≠0），与x轴的另一交点为E，连结CE，点A、B、D的坐标分别为（﹣2，0）、（3，0）、（0，4）．
1. （1）求抛物线的解析式；
2. （2）已知抛物线的对称轴l交x轴于点F，交线段CD于点K，点M、N分别是直线l和x轴上的动点，连结MN，当线段MN恰好被BC垂直平分时，求点N的坐标；
3. （3）在满足（2）的条件下，过点M作一条直线，使之将四边形AECD的面积分为3：4的两部分，求出该直线的解析式．
答案解析收藏纠错 + 选题