 B .
B .  C .
C .  D .
D . 
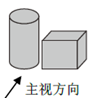
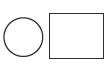 B .
B .  C .
C . 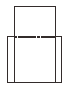 D .
D . 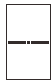
40,38,42,35,45,40,42,42,则这组数据的众数与中位数分别是( )
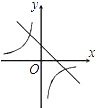 B .
B . 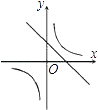 C .
C . 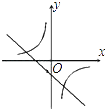 D .
D . 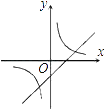
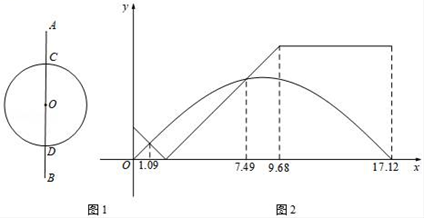
①小王的运动路程比小林的长②两人分别在1.09秒和7.49秒的时刻相遇③当小王运动到点D的时候,小林已经过了点D④在4.84秒时,两人的距离正好等于⊙O的半径上述说法正确的个数的是( )

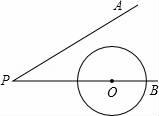



(结果精确到0.1m . 参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
|
成绩x/分 |
频数 |
频率 |
|
50≤x<60 |
5 |
0.05 |
|
60≤x<70 |
10 |
0.10 |
|
70≤x<80 |
a |
0.15 |
|
80≤x<90 |
30 |
b |
|
90≤x≤100 |
40 |
0.40 |
请根据所给的信息,解答下列问题:



操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH .
操作2:过点G作CD∥AB,使点D、点C分别落在边AF , BE上.则四边形ABCD为 矩形.
如图b , O是对角线AC的中点,若点N在边BC上,
,连接
求
的值;
连结AC,CM,当△AMC为等腰三角形时,将△CBM沿着CM翻折,点B的对称点为B’,连结AB’
求 的值.

求a、b、m满足的关系式;
当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为5,请你探究a的取值范围.