 B .
B .  C .
C .  D .
D . 

 C .
C . 
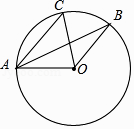
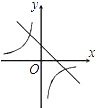 B .
B . 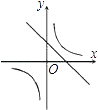 C .
C . 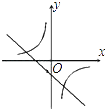 D .
D . 




|
成绩x/分 |
频数 |
频率 |
|
50≤x<60 |
5 |
0.05 |
|
60≤x<70 |
10 |
0.10 |
|
70≤x<80 |
a |
0.15 |
|
80≤x<90 |
30 |
b |
|
90≤x≤100 |
40 |
0.40 |
请根据所给信息,解答下列问题:



下面,我们通过折叠的方式折出一个 矩形,如图a所示.
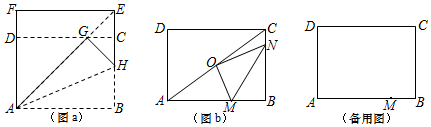
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为 矩形.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求 的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2 ,则DR的最小值=.

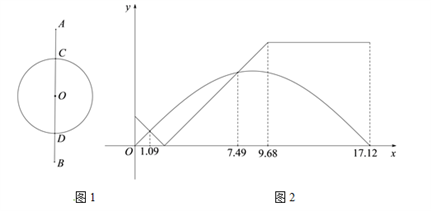
①求a、b、m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为5,请你探究a的取值范围.