2017年江西省鹰潭市中考数学模拟试卷

更新时间：2017-07-07 浏览次数：823 类型：中考模拟

一、选择题

1. (2017·鹰潭模拟) 李刚同学拿一个矩形木框在阳光下摆弄，矩形木框在地面上形成的投影不可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2017·五莲模拟) 如果不等式组 $\text{[math]}$ 恰有3个整数解，则a的取值范围是（　　）

A . a≤﹣1 B . a＜﹣1 C . ﹣2≤a＜﹣1 D . ﹣2＜a≤﹣1

答案解析收藏纠错 + 选题
3. (2020·安阳模拟) 如图，是某几何体的三视图及相关数据，则该几何体的侧面积是（）

A . 10π B . 15π C . 20π D . 30π

答案解析收藏纠错 + 选题
4. (2023九下·北仑模拟) 互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为（　　）

A . 120元 B . 100元 C . 80元 D . 60元

答案解析收藏纠错 + 选题
5. 如图所示，向一个半径为R、容积为V的球形容器内注水，则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2017·东明模拟) 如图：二次函数y=ax2+bx+c的图象所示，下列结论中：①abc＞0；②2a+b=0；③当m≠1时，a+b＞am²+bm；④a﹣b+c＞0；⑤若ax₁²+bx₁=ax₂²+bx₂ ，且x₁≠x₂ ，则x₁+x₂=2，正确的个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题：

7. (2021·东台模拟) 分解因式：a³﹣2a²+a=．

答案解析收藏纠错 + 选题
8. (2020九上·建华期末) 若 $\text{[math]}$ tan（x+10°）=1，则锐角x的度数为．

答案解析收藏纠错 + 选题
9. (2017·鹰潭模拟) 如图：M为反比例函数 $\text{[math]}$ 图象上一点，MA⊥y轴于A，S_△_MAO=2时，k=．

答案解析收藏纠错 + 选题
10. (2024八下·滨海月考) 关于x的分式方程 $\text{[math]}$ 的解为正数，则m的取值范围是．

答案解析收藏纠错 + 选题
11. (2017·鹰潭模拟) 在平行四边形ABCD中，E是CD上一点，DE：EC=1：3，连AE，BE，BD且AE，BD交于F，则S_△_DEF：S_△_EBF：S_△_ABF=．

答案解析收藏纠错 + 选题
12. (2017·鹰潭模拟) 两个反比例函数y= $\text{[math]}$ （k＞1）和y= $\text{[math]}$ 在第一象限内的图象如图所示，点P在y= $\text{[math]}$ 的图象上，PC⊥x轴于点C，交y= $\text{[math]}$ 的图象于点A，PD⊥y轴于点D，交y= $\text{[math]}$ 的图象于点B，BE⊥x轴于点E，当点P在y= $\text{[math]}$ 图象上运动时，以下结论：①BA与DC始终平行；②PA与PB始终相等；③四边形PAOB的面积不会发生变化；④△OBA的面积等于四边形ACEB的面积．其中一定正确的是（填序号）

答案解析收藏纠错 + 选题

三、解答题：

13. (2017·鹰潭模拟) 计算下列各题
1. （1） $\text{[math]}$ ﹣3tan30°+（4﹣π）⁰﹣（ $\text{[math]}$ ）^﹣¹
2. （2）先化简，再求值：（ $\text{[math]}$ ﹣x+1）÷ $\text{[math]}$ ，其中x= $\text{[math]}$ ﹣2．
答案解析收藏纠错 + 选题
14. (2017·鹰潭模拟) 在一个木箱中装有卡片共50张，这些卡片共有三种，它们分别标有1、2、3的字样，除此之外其他都相同，其中标有数字2的卡片的张数是标有数字3卡片的张数的3倍少8张．已知从箱子中随机摸出一张标有数字1卡片的概率是 $\text{[math]}$ ．
1. （1）求木箱中装有标1的卡片张数；
2. （2）求从箱子中随机摸出一张标有数字3的卡片的概率．
答案解析收藏纠错 + 选题
15. (2017·鹰潭模拟)
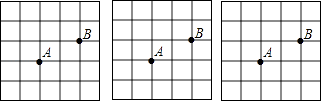
已知下面是3个5×5的正方形网格，小正方形边长都为1，A、B两点在小网格的顶点上，位置如图所示．现请你分别在三个网格中各画一个△ABC．要求：（1）顶点C在网格的顶点上；（2）工具只用无刻度的直尺；（3）所画的3个三角形互不全等，但面积都为2．

答案解析收藏纠错 + 选题
16. (2017七下·东城期中) 某校食堂的中餐与晚餐的资费标准如下：
种类
单价
米饭
0.5元/份
A类套餐菜
3.5元/份
B类套餐菜
2.5元/份
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐，这五天共消费36元．请问小杰在这五天内，A，B类套餐菜各选用了多少次？

答案解析收藏纠错 + 选题
17. (2017·鹰潭模拟)
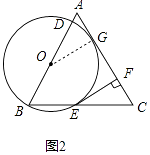
如图是放在水平地面上的一把椅子的侧面图，椅子高为AC，椅面宽为BE，椅脚高为ED，且AC⊥BE，AC⊥CD，AC∥ED．从点A测得点D、E的俯角分别为64°和53°．已知ED=35cm，求椅子高AC约为多少？
（参考数据：tan53°≈ $\text{[math]}$ ，sin53°≈ $\text{[math]}$ ，tan64°≈2，sin64°≈ $\text{[math]}$ ）

答案解析收藏纠错 + 选题

四、解答题：

18. (2017·鹰潭模拟)
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）．
1. （1） ①画出△ABC关于y轴对称的图形△A₁B₁C₁ ，并直接写出C₁点坐标；
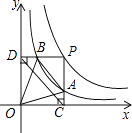
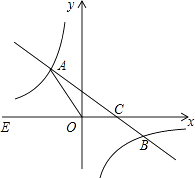
  ②以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A₂B₂C₂ ，并直接写出C₂点坐标；
2. （2）如果点D（a，b）在线段AB上，请直接写出经过（1）②的变化后点D的对应点D₂的坐标．
答案解析收藏纠错 + 选题
19. (2017·鹰潭模拟) 已知：如图1，△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F．
1. （1）求证：直线EF是⊙O的切线；
2. （2）如图2，当直线AC与⊙O相切时，求⊙O的半径．
答案解析收藏纠错 + 选题
20. (2017·鹰潭模拟) 某地区在一次九年级数学做了检测中，有一道满分8分的解答题，按评分标准，所有考生的得分只有四种：0分，3分，5分，8分．老师为了了解学生的得分情况与题目的难易情况，从全区4500名考生的试卷中随机抽取一部分，通过分析与整理，绘制了如下两幅图不完整的统计图．
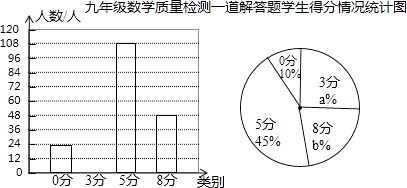
请根据以上信息解答下列问题：
1. （1）填空：a=，b=，并把条形统计图补全；
2. （2）请估计该地区此题得满分（即8分）的学生人数；
3. （3）已知难度系数的计算公式为L= $\text{[math]}$ ，其中L为难度系数，X为样本平均得分，W为试题满分值．一般来说，根据试题的难度系数可将试题分为以下三类：当0＜L≤0.4时，此题为难题；当0.4＜L≤0.7时，此题为中等难度试题；当0.7＜L＜1时，此题为容易题．试问此题对于该地区的九年级学生来说属于哪一类？
答案解析收藏纠错 + 选题

五、解答题：

21. (2017·鹰潭模拟) 如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数 $\text{[math]}$ 的图象交于二四象限内的A、B 两点，与x轴交于C点，点B的坐标为（6，n），线段OA=5，E为x轴负半轴上一点，且sin∠AOE= $\text{[math]}$ ．
1. （1）求该反比例函数和一次函数的解析式；
2. （2）求△AOC的面积；
3. （3）直接写出一次函数值大于反比例函数值时自变量x的取值范围．
答案解析收藏纠错 + 选题
22. (2017·鹰潭模拟)
如图，已知四边形ABCD为正方形，AB=2 $\text{[math]}$ ，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．
1. （1）求证：矩形DEFG是正方形；
2. （2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由；
3. （3）设AE=x，四边形DEFG的面积为S，求出S与x的函数关系式．
答案解析收藏纠错 + 选题

六、解答题：

23. (2017·鹰潭模拟)
如图1，抛物线C：y=x²经过变化可得到抛物线C₁：y₁=a₁x（x﹣b₁），C₁与x轴的正半轴交与点A₁ ，且其对称轴分别交抛物线C，C₁于点B₁ ， D₁ ，此时四边形OB₁A₁D₁恰为正方形；按上述类似方法，如图2，抛物线C₁：y₁=a₁x（x﹣b₁）经过变换可得到抛物线C₂：y₂=a₂x（x﹣b₂），C₂与x轴的正半轴交与点A₂ ，且其对称轴分别交抛物线C₁ ， C₂于点B₂ ， D₂ ，此时四边形OB₂A₂D₂也恰为正方形；按上述类似方法，如图3，可得到抛物线C₃：y₃=a₃x（x﹣b₃）与正方形OB₃A₃D₃ ．请探究以下问题：
1. （1）填空：a₁=，b₁=；
2. （2）求出C₂与C₃的解析式；
3. （3）按上述类似方法，可得到抛物线C_n：y_n=a_nx（x﹣b_n）与正方形OB_nA_nD_n（n≥1）．
  ①请用含n的代数式直接表示出C_n的解析式；
  ②当x取任意不为0的实数时，试比较y₂₀₁₅与y₂₀₁₆的函数值的大小并说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2017年江西省鹰潭市中考数学模拟试卷

副标题：

*注意事项：

2017年江西省鹰潭市中考数学模拟试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

种类	单价
米饭	0.5元/份
A类套餐菜	3.5元/份
B类套餐菜	2.5元/份