
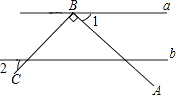

 B .
B .  C .
C .  D .
D . 
①同位角相等;②经过直线外一点有且只有一条直线与这条直线平行;③长度相等的弧是等弧;④顺次连接菱形各边中点得到的四边形是矩形.

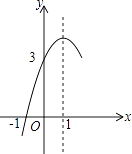

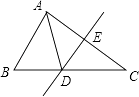

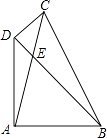


请你根据以上的信息,回答下列问题:

如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6 米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.


附:阅读材料
法国弗朗索瓦•韦达最早发现一元二次方程中根与系数的关系为:两根之和等于一次项系数与二次项系数之比的相反数,两根之积等于常数项羽二次项系数之比,人们称之为韦达定理.
即:设一元二次方程ax2+bx+c=0的两根为x1、x2 , 则:x1+x2=﹣ ,x1•x2=
能灵活运用韦达定理,有时可以使解题更为简单.
