2017年河南省南阳市唐河县中考数学一模试卷

更新时间：2024-07-12 浏览次数：1260 类型：中考模拟

一、选择题

1. (2017·唐河模拟) 有理数﹣ $\text{[math]}$ 的相反数的倒数是（）

A . ﹣ $\text{[math]}$ B . ﹣ $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2017·唐河模拟) 据统计，2017年高新技术产品出口总额达50570亿元，将数据50570亿用科学记数法表示为（）

A . 5.0570×10⁹ B . 0.50570×10¹⁰ C . 50.570×10¹¹ D . 5.0570×10¹²

答案解析收藏纠错 + 选题
3. (2021·绵竹模拟) 如图是将正方体切去一个角后形成的几何体，则该几何体的左视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·宁波模拟) 某中学为了让学生的跳远在中考体育测试中取得满意的成绩，在锻炼一个月后，学校对九年级一班的45名学生进行测试，成绩如下表：
跳远成绩（cm）
160
170
180
190
200
220
人数
3
9
6
9
15
3
这些运动员跳远成绩的中位数和众数分别是（）

A . 190，200 B . 9，9 C . 15，9 D . 185，200

答案解析收藏纠错 + 选题
5. (2018·霍邱模拟) 如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（）

A . 7 B . 8 C . 9 D . 10

答案解析收藏纠错 + 选题
6. (2019九上·宝应期末) 关于x的一元二次方程x²﹣ $\text{[math]}$ x+sinα=0有两个相等的实数根，则锐角α等于（）

A . 15° B . 30° C . 45° D . 60°

答案解析收藏纠错 + 选题
7. (2021九上·湖州月考) 一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4随机摸出一个小球，不放回，再随机摸出一个小球，两次摸出的小球标号的积小于4的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2017·唐河模拟) 抛物线y=ax²+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y= $\text{[math]}$ 在同一平面直角坐标系内的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2017·唐河模拟)
如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°则第30秒时，菱形的对角线交点D的坐标为（）

A . （1，﹣1） B . （﹣1，﹣1） C . （ $\text{[math]}$ ，0） D . （0，﹣ $\text{[math]}$ ）

答案解析收藏纠错 + 选题
10. (2017·谷城模拟) 如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是 $\text{[math]}$ 上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（）

A . 15° B . 20° C . 25° D . 30°

答案解析收藏纠错 + 选题

二、填空题

11. (2017·唐河模拟) 计算： $\text{[math]}$ ﹣（π﹣3）⁰﹣10sin30°﹣（﹣1）²⁰¹⁷+ $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2023七下·北辰期中) 如图，直线a∥b，∠1=120°，∠2=40°，则∠3等于．

答案解析收藏纠错 + 选题
13. (2020九上·兰州期末) 如图，抛物线y₁=a（x+2）²+m过原点，与抛物线y₂= $\text{[math]}$ （x﹣3）²+n交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．下列结论：①两条抛物线的对称轴距离为5；②x=0时，y₂=5；③当x＞3时，y₁﹣y₂＞0；④y轴是线段BC的中垂线．正确结论是（填写正确结论的序号）．

答案解析收藏纠错 + 选题
14. (2017·泰兴模拟) 如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是．

答案解析收藏纠错 + 选题
15. (2018·镇平模拟) 如图，矩形ABCD中，AB=1，AD=2，点E是边AD上的一个动点，把△BAE沿BE折叠，点A落在A′处，如果A′恰在矩形的对称轴上，则AE的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2017·唐河模拟) 先化简，再求值： $\text{[math]}$ ，其中x的值是不等式组 $\text{[math]}$ 的整数解．

答案解析收藏纠错 + 选题
17. (2017·唐河模拟) 某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过调查获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：
1. （1）这次活动一共调查了名学生；
2. （2）补全条形统计图；
3. （3）在扇形统计图中，选择篮球项目的人数所在扇形的圆心角等于度；
4. （4）若该学校有1500人，请你估计该学校选择足球项目的学生人数约是人．
答案解析收藏纠错 + 选题
18. (2017·唐河模拟) 如图，在Rt△ABC中，∠ABC=90°，点M是AC的中点，以AB为直径做⊙O分别交AC，BM于点D、E．
1. （1）求证：∠MDE=∠MED；
2. （2）填空：
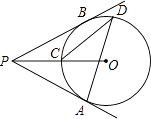
  ①若AB=6，当DM=2AD时，DE=；
  ②连接OD、OE，当∠C的度数为时，四边形ODME是菱形．
答案解析收藏纠错 + 选题
19. (2017·唐河模拟)
如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF=3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．
（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．

答案解析收藏纠错 + 选题
20. (2017·唐河模拟) 阅读下面材料：如图1，在平面直角坐标系xOy中，直线y₁=ax+b与双曲线y₂= $\text{[math]}$ 交于A（1，3）和B（﹣3，﹣1）两点，观察图象可知：①当x=﹣3或1时，y₁=y₂；②当﹣3＜x＜0或x＞1时，y₁＞y₂；即通过观察函数的图象，可以得到不等式ax+b＞ $\text{[math]}$ 的解集．

有这样一个问题：求不等式x³+4x²﹣x﹣4＞0的解集．

艾斯柯同学类比以上知识的研究方法，用函数与方程的思想对不等式的解法进行了探究，请将他下面的②③④补充完整：

①当x=0时，原不等式不成立：当x＞0时，原不等式可以转化为x²+4x﹣1＞ $\text{[math]}$ ；当x＜0时，原不等式可以转化为x²+4x﹣1＜ $\text{[math]}$ ．

②构造函数，画出图象

设y₃=x²+4x﹣1，y₄= $\text{[math]}$ 在同一坐标系中分别画出这两个函数的图象．

双曲线y₄= $\text{[math]}$ 如图2所示，请在此坐标系中直接画出抛物线y₃=x²+4x﹣1（可不列表）；

③利用图象，确定交点横坐标

观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y₃=y₄的所有x的值为 $\text{[math]}$

④借助图象，写出解集

结合（1）的讨论结果，观察两个函数的图象可知：不等式x³+4x²﹣x﹣4＞0的解集为 $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2017·唐河模拟) 某微店销售甲、乙两种商品，卖出6件甲商品和4件乙商品可获利120元；卖出10件甲商品和6件乙商品可获利190元．
1. （1）甲、乙两种商品每件可获利多少元？
2. （2）若该微店甲、乙两种商品预计再次进货200件，全部卖完后总获利不低于2300元，已知甲商品的数量不少于120件．请你帮忙设计一个进货方案，使总
答案解析收藏纠错 + 选题
22. (2017·唐河模拟) 综合题。
1. （1）
  问题发现：
  如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为
2. （2）
  拓展探究：
  在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE、CE、AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
3. （3）问题解决：
  当正方形CDEF旋转到B、E、F三点共线时候，直接写出线段AF的长．
答案解析收藏纠错 + 选题
23. (2020·武威模拟)
如图，抛物线y=﹣x²+bx+c与x轴相交于A、B两点，与y轴相交于点C，且点B与点C的坐标分别为B（3，0）．C（0，3），点M是抛物线的顶点．
1. （1）求二次函数的关系式；
2. （2）点P为线段MB上一个动点，过点P作PD⊥x轴于点D．若OD=m，△PCD的面积为S，试判断S有最大值或最小值？并说明理由；
3. （3）在MB上是否存在点P，使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．
答案解析收藏纠错 + 选题