如图所示的是三通管的立体图,则这个几何体的俯视图是( )
 B .
B .  C .
C .  D .
D . 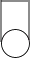
跳远成绩(cm) | 160 | 170 | 180 | 190 | 200 | 220 |
人数 | 3 | 9 | 6 | 9 | 15 | 3 |
这些运动员跳远成绩的中位数和众数分别是( )
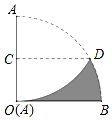


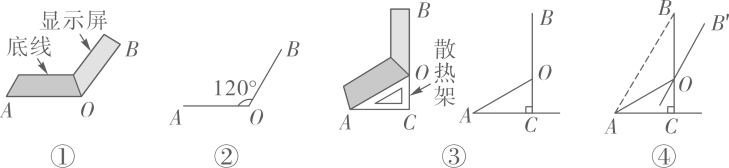

如图2, 与
是偏等积三角形,
,
,且线段
的长度为正整数,过点
作
交
的延长线于点
,求
的长度;
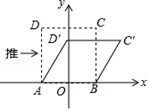
如图3,四边形 是一片绿色花园,
、
是等腰直角三角形,
(
).
① 与
是偏等积三角形吗?请说明理由;
②已知 ,
的面积为
.如图4,计划修建一条经过点
的笔直的小路
,
在
边上,
的延长线经过
中点
.若小路每米造价600元,请计算修建小路的总造价.