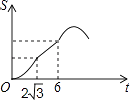
如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
 B .
B . 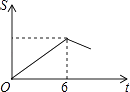 C .
C . 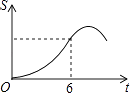 D .
D . 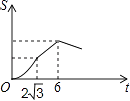
比如:2⊕5=2×(2﹣5)+1
=2×(﹣3)+1
=﹣6+1
=﹣5
若3⊕x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
![]()
如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.

当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.

如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25

①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, 为半径的圆的方程为.
如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= .

①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
如图1所示,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).