湖北省鄂州市梁子湖区2019届九年级上学期数学期末考试试卷

更新时间：2024-07-13 浏览次数：257 类型：期末考试

一、单选题

1. (2023九上·卢龙期末) 方程x²＝2x的解是（）

A . x＝2 B . x＝0 C . x₁＝2，x₂＝0 D . x₁＝ $\text{[math]}$ ，x₂＝0

答案解析收藏纠错 + 选题
2. (2022八下·南海期末) 如图汽车标志中不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九上·当阳月考) 某超市一月份营业额为100万元，一月、二月、三月的营业额共500万元，如果平均每月增长率为x，则由题意可列方程（　　）

A . 100（1+x）²＝500 B . 100+100•2x＝500 C . 100+100•3x＝500 D . 100[1+（1+x）+（1+x）²]＝500

答案解析收藏纠错 + 选题
4. (2018九上·梁子湖期末) 一个十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒.当你抬头看信号灯时，是绿灯的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2018九上·梁子湖期末) 如图，在△ABC中，∠CAB＝30°，将△ABC在平面内绕点A逆时针旋转到△AB'C'的位置，且CC'∥AB，则旋转角的度数为（　　）

A . 100° B . 120° C . 110° D . 130°

答案解析收藏纠错 + 选题
6. (2018九上·梁子湖期末) 如图，在矩形ABCD中，AB＝8，AD＝12，经过A，D两点的⊙O与边BC相切于点E，则⊙O的半径为（　　）

A . 4 B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2018九上·梁子湖期末) 如图，点A是反比例函数 $\text{[math]}$ 在第二象限内图象上一点，点B是反比例函数 $\text{[math]}$ 在第一象限内图象上一点，直线AB与y轴交于点C，且AC＝BC，连接OA、OB，则△AOB的面积是（　　）

A . 2 B . 2.5 C . 3 D . 3.5

答案解析收藏纠错 + 选题
8. (2018九上·梁子湖期末) 如图，半径为5的⊙A中，DE＝2 $\text{[math]}$ ，∠BAC+∠EAD＝180°，则弦BC的长为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 $\text{[math]}$ D . 3 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·广汉模拟) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点A（-1，0），顶点坐标（1，n）与 $\text{[math]}$ 轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③对于任意实数m，a+b≥am²+bm总成立；④关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个不相等的实数根.其中结论正确的个数为 $\text{[math]}$ 　　 $\text{[math]}$

A . 1 个 B . 2 个 C . 3 个 D . 4 个

答案解析收藏纠错 + 选题
10. (2021·靖江模拟) 如图，一次函数y=2x与反比例函数y= $\text{[math]}$ （k＞0）的图象交于A，B两点，点P在以C（﹣2，0）为圆心，1为半径的⊙C上，Q是AP的中点，已知OQ长的最大值为 $\text{[math]}$ ，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2018九上·梁子湖期末) 如图，在△ABC中，∠ACB=90°，过B，C两点的⊙O交AC于点D，交AB于点E，连接EO并延长交⊙O于点F.连接BF，CF.若∠EDC=135°，CF= $\text{[math]}$ ，则AE²+BE²的值为（）

A . 8 B . 12 C . 16 D . 20

答案解析收藏纠错 + 选题

二、填空题

12. (2021九上·临沭期中) 若n（n≠0）是关于x的方程x²+mx+2n=0的根，则m+n的值为.

答案解析收藏纠错 + 选题
13. (2020九上·温州月考) 从长度分别为2，4，6，7的四条线段中随机取三条，能构成三角形的概率是

答案解析收藏纠错 + 选题
14. (2018九上·梁子湖期末) 如图，从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形，再将剪下的扇形围成一个圆锥，则圆锥的底面半径为m．

答案解析收藏纠错 + 选题
15. (2023九上·琅琊月考) 当a﹣1≤x≤a时，函数y＝x²﹣2x+1的最小值为1，则a的值为.

答案解析收藏纠错 + 选题
16. (2018九上·梁子湖期末) 如图抛物线y=x²+2x﹣3与x轴交于A，B两点，与y轴交于点C，点P是抛物线对称轴上任意一点，若点D、E、F分别是BC、BP、PC的中点，连接DE，DF，则DE+DF的最小值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·南海月考) 解下列方程：
1. （1） x²+3x﹣2＝0；
2. （2） 2（x﹣3）²＝x²﹣9
答案解析收藏纠错 + 选题
18. (2018九上·梁子湖期末) 将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG.
1. （1）如图，当点E在BD上时.求证：FD＝CD；
2. （2）当α为何值时，GC＝GB？画出图形，并说明理由.
答案解析收藏纠错 + 选题

19. (2018九上·梁子湖期末) “品中华诗词，寻文化基因”.某校举办了第二届“中华诗词大赛”，将该校八年级参加竞赛的学生成绩统计后，绘制了如下不完整的频数分布统计表与频数分布直方图.

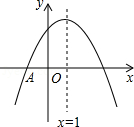
频数分布统计表

组别	成绩x（分）	人数	百分比
A	60≤x＜70	8	20%
B	70≤x＜80	16	m%
C	80≤x＜90	a	30%
D	90≤＜x≤100	4	10%

请观察图表，解答下列问题：

（1）表中a=，m=；
（2）补全频数分布直方图；
（3） D组的4名学生中，有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛，则抽取的2名学生恰好是一名男生和一名女生的概率是？

答案解析收藏纠错 + 选题

20. (2020七上·呼和浩特月考) 已知关于x的一元二次方程x²+（k﹣5）x+1﹣k=0（其中k为常数）.
1. （1）求证无论k为何值，方程总有两个不相等实数根；
2. （2）已知函数y=x²+（k﹣5）x+1﹣k的图象不经过第三象限，求k的取值范围；
3. （3）若原方程的一个根大于3，另一个根小于3，求k的最大整数值.
答案解析收藏纠错 + 选题
21. (2018九上·梁子湖期末) 如图，直线y＝k₁x（x≥0）与双曲线y＝ $\text{[math]}$ （x＞0）相交于点P（2，4）.已知点A（4，0），B（0，3），连接AB，将Rt△AOB沿OP方向平移，使点O移动到点P，得到△A'PB'.过点A'作A'C∥y轴交双曲线于点C.
1. （1）求k₁与k₂的值；
2. （2）求直线PC的表达式；
3. （3）直接写出线段AB扫过的面积.
答案解析收藏纠错 + 选题
22. (2018九上·梁子湖期末) 如图，已知AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE.
1. （1）求证：AC平分∠DAB；
2. （2）求证：△PCF是等腰三角形；
3. （3）若AF=6，EF=2 $\text{[math]}$ ，求⊙O的半径长.
答案解析收藏纠错 + 选题

23. (2018九上·梁子湖期末) 温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元.根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元.设每天安排x人生产乙产品.

（1）根据信息填表

产品种类	每天工人数（人）	每天产量（件）	每件产品可获利润（元）
甲			15
乙	$\text{[math]}$

（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润.
（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的x值.

答案解析收藏纠错 + 选题

24. (2018九上·梁子湖期末) 如图，已知直线y＝﹣x+4分别交x轴、y轴于点A、B，抛物线过y＝ax²+bx+c经过A，B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．
1. （1）若抛物线的解析式为y＝﹣ $\text{[math]}$ x²+x+4，设其顶点为M，其对称轴交AB于点N．
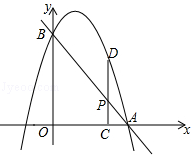
  ①求点M、N的坐标；
  
  ②是否存在点P，使四边形MNPD为菱形？并说明理由；
2. （2）当点P的横坐标为2时，是否存在这样的抛物线，使得以B、P、D为顶点的三角形是直角三角形？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

湖北省鄂州市梁子湖区2019届九年级上学期数学期末考试试卷

副标题：

*注意事项：

湖北省鄂州市梁子湖区2019届九年级上学期数学期末考试试卷

试题分析

总体分析

题量分析

难度分析

知识点分析