福建省南平市育才中学2016-2017学年七年级下学期期末复...

图①是一块边长为1，周长记为P₁的正三角形纸板，沿图①的底边剪去一块边长为 的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪掉正三角形纸板边长的 ）后，得图③，④，…，记第n(n≥3) 块纸板的周长为P_n ， 则P_n-P_n-1的值为（       ）

如图，小明作出了边长为1的第1个正△A₁B₁C₁ ， 算出了正△A₁B₁C₁的面积。然后分别取△A₁B₁C₁的三边中点A₂、B₂、C₂ ， 作出了第2个正△A₂B₂C₂ ， 算出了正△A₂B₂C₂的面积。用同样的方法，作出了第3个正△A₃B₃C₃ ， 算出了正△A₃B₃C₃的面积……，由此可得，第10个正△A₁₀B₁₀C₁₀的面积是（       ）

如图，菱形ABCD中，点M，N在AC上，ME⊥AD， NF⊥AB. 若NF = NM = 2，ME = 3，则AN =（       ）

袋中放有一套（五枚）北京2008年奥运会吉祥物福娃纪念币，依次取出（不放回）两枚纪念币，恰好能够组成“欢迎”的概率是 （       ）

已知，如图，△ABC中，∠B=∠DAC，则∠BAC和∠ADC的关系是（       ）

在一次数学综合实践课上，某同学将一张等边三角形纸片沿中位线剪成4个小三角形．称为第一次操作；然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是（   ）

如图，将矩形ABCD纸片沿对角线BD折叠，使点C落在 处， 交AD于E，若 ，则在不添加任何辅助线的情况下，图中 的角（虚线也视为角的边）有（       ）

如图，等边三角形△OAB₁的一边OA在 x 轴上，且OA=1，当△OAB₁沿直线l滚动，使一边与直线l重合得到△B₁A₁B₂ ， △B₂A₂B₃ ， ......则点A₂₀₁₇的坐标是．

如图，△ABC中，AB=AC，AD是∠BAC的平分线，若△ABD的周长为12，△ABC的周长为16，则AD的长为．

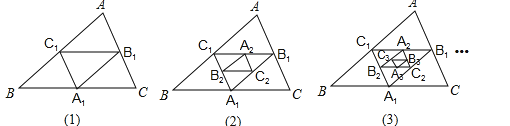
如图，在图（1）中，A₁、B₁、C₁分别是△ABC的边BC、CA、AB的中点，在图（2）中，A₂、B₂、C₂分别是△A₁B₁C₁的边B₁C₁、C₁A₁、A₁B₁的中点，…，按此规律，则第n个图形中平行四边形的个数共有个

如图，是某射手在相同条件下进行射击训练的结果统计图，该射手击中靶心的概率的估计值为．

把一副三角板如图甲放置，其中 ， ，斜边AB=6cm，DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D₁CE₁（如图乙）．这时AB与CD₁相交于点O，与D₁E₁相交于点F ．

如图，CD是△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处．

如图所示，AB=AE，∠ABC=∠AED，BC=ED，点F是CD的中点。