2015年高考理数真题试卷（陕西卷）

更新时间：2016-08-16 浏览次数：723 类型：高考真卷

一、选择题：在每小题给出的四个选项中，只有一项符合题目要求，（本大题共12小题，每小题5分，共60分）

1. 设集合M={x|x²=x}，N={x|lgx≤0}，则M $\text{[math]}$ N（）

A . [0，1] B . (0，1] C . [0，1) D . (- $\text{[math]}$ ， 1]

答案解析收藏纠错 + 选题
2.
某中学初中部共有110名教师，高中部共有150名教师，其性别比例如图所示，则该校女教师的人数为（）

A . 167 B . 137 C . 123 D . 93

答案解析收藏纠错 + 选题
3.
如图，某港口一天6时到18时的水深变化曲线近似满足函数y=3sin( $\text{[math]}$ x+ $\text{[math]}$ )+k，据此函数可知，这段时间水深（单位：m）的最大值为（）

A . 5 B . 6 C . 8 D . 10

答案解析收藏纠错 + 选题
4. 二项式 $\text{[math]}$ $\text{[math]}$ 的展开式中x²的系数为15，则n=（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
5. (2020高二上·鹤岗月考)
一个几何体的三视图如图所示，则该几何体的表面积为（）

A . 3 $\text{[math]}$ B . 4 $\text{[math]}$ C . 2 $\text{[math]}$ +4 D . 3 $\text{[math]}$ +4

答案解析收藏纠错 + 选题
6. “sin $\text{[math]}$ =cos $\text{[math]}$ ”是“cos2 $\text{[math]}$ =0”的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充分必要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
7. 对任意向量 $\text{[math]}$ ，下列关系式中不恒成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8.
根据如图框图，当输入x为2006时，输出的y=（　　）

A . 28 B . 10 C . 4 D . 2

答案解析收藏纠错 + 选题
9. (2020高二上·千阳期中) 设f(x)=lnx， 0<a<b，若p=f( $\text{[math]}$ )，q=f( $\text{[math]}$ )，r= $\text{[math]}$ (f(a)+f(b))，则下列关系式中正确的是（）

A . q=r<p B . q=r>p C . p=r<q D . p=r>q

答案解析收藏纠错 + 选题
10. 某企业生产甲、乙两种产品均需用A，B两种原料．已知生产1吨每种产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为（）

甲
乙
原料限额
A（吨）
3
2
12
B（吨）
1
2
8

A . 12万元 B . 16万元 C . 17万元 D . 18万元

答案解析收藏纠错 + 选题
11. 设复数z=(x-1)+yi(x， y $\text{[math]}$ R)，若|z|≤1，则y≥x的概率为（）

A . $\text{[math]}$ + $\text{[math]}$ B . $\text{[math]}$ - $\text{[math]}$ C . $\text{[math]}$ - $\text{[math]}$ D . $\text{[math]}$ + $\text{[math]}$

答案解析收藏纠错 + 选题
12. 对二次函数f（x）=ax²+bx+c（a为非零常数），四位同学分别给出下列结论，其中有且仅有一个结论是错误的，则错误的结论是（）

A . -1是f(x)的零点 B . 1是f(x)的极值点 C . 3是f(x)的极值 D . 点(2,8)在曲线y=f(x) 上

答案解析收藏纠错 + 选题

二、填空题：把答案填写在答题卡相应题号后的横线上（本大题共4小题，每小题5分，共20分）

13. 中位数1010的一组数构成等差数列，其末项为2015，则该数列的首项为．

答案解析收藏纠错 + 选题
14. 若抛物线y²=2px(p>0)的准线经过双曲线x²-y²=1的一个焦点，则p= ．

答案解析收藏纠错 + 选题
15. 设曲线y=e^x在点（0，1）处的切线与曲线y= $\text{[math]}$ (x>0)上点P处的切线垂直，则P的坐标为。

答案解析收藏纠错 + 选题
16.
如图，一横截面为等腰梯形的水渠，因泥沙沉积，导致水渠截面边界呈抛物线型（图中虚线表示），则原始的最大流量与当前最大流量的比值为．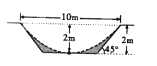

答案解析收藏纠错 + 选题

三、解答题：解答应写出文字说明，证明过程或演算步骤（本大题共6小题，共70分）

17. (2024高一下·乌鲁木齐期中) △ABC的内角A，B，C所对的边分别为a，b，c．向量 $\text{[math]}$ 与 $\text{[math]}$ 平行．
1. （1）求A。
2. （2）若a= $\text{[math]}$ ， b=2求△ABC的面积。
答案解析收藏纠错 + 选题
18.
如图1，在直角梯形ABCD中，AD∥BC， $\text{[math]}$ BAD= $\text{[math]}$ ， AB=BC=1，AD=2， E是AD的中点，0是AC与BE的交点．将△ABE沿BE折起到△A₁BE的位置，如图2．
1. （1）证明：CD⊥平面A₁OC
2. （2）若平面A₁BE⊥平面BCDE，求平面A₁BC与平面A₁CD夹角的余弦值.
答案解析收藏纠错 + 选题
19. 设某校新、老校区之间开车单程所需时间为T，T只与道路畅通状况有关，对其容量为100的样本进行统计，结果如下：
T（分钟）
25
30
35
40
频数（次）
20
30
40
10
1. （1）求T的分布列与数学期望ET；
2. （2）刘教授驾车从老校区出发，前往新校区做一个50分钟的讲座，结束后立即返回老校区，求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率．
答案解析收藏纠错 + 选题
20. 已知椭圆E： $\text{[math]}$ （a>b>0）的半焦距为c，原点0到经过两点(c，0)，(0，b)的直线的距离为 $\text{[math]}$ c．
1. （1）求椭圆E的离心率
2. （2）
  如图，AB是圆M：（x+2）²+（y-1)= $\text{[math]}$ 的一条直径，若椭圆E经过A，B两点，求椭圆E的方程．
答案解析收藏纠错 + 选题
21. 设f_n(x)是等比数列1，x，x²...，xⁿ的各项和，其中x>0，n $\text{[math]}$ N，，n≥2，
1. （1）证明：函数F_n（x）=f_n(x)-2在( $\text{[math]}$ ， 1)内有且仅有一个零点（记为x_n），且x_n= $\text{[math]}$ + $\text{[math]}$ x_nⁿ⁺¹；
2. （2）设有一个与上述等比数列的首项、末项、项数分别相同的等差数列，其各项和为g_n(x)，比较f_n(x)与g_n(x)的大小，并加以证明．
答案解析收藏纠错 + 选题
22.
如图，AB切 $\text{[math]}$ O于点D，直线AD交 $\text{[math]}$ O于D，E两点，BC⊥DE，垂足为C．
1. （1）证明： $\text{[math]}$ CBD= $\text{[math]}$ DBA；
2. （2）若AD=3DC，BC= $\text{[math]}$ ，求 $\text{[math]}$ O的直径．
答案解析收藏纠错 + 选题
23. 在直角坐标系xOy中，直线l的参数方程为 $\text{[math]}$ （t为参数）．以原点为极点，x轴正半轴为极轴建立极坐标系， $\text{[math]}$ c的极坐标方程为 $\text{[math]}$ =2 $\text{[math]}$ sin $\text{[math]}$ ．
1. （1）写出 $\text{[math]}$ c的直角坐标方程；
2. （2） P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．
答案解析收藏纠错 + 选题
24. 选修4-5：不等式选讲, 已知关于x的不等式|x+a|<b的解集为{x|2<x<4}．
1. （1）求实数a，b的值；
2. （2）求 $\text{[math]}$ + $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题